Ортогональные операторы

В комплексных унитарных пространствах рассматривались унитарные операторы, т.е. операторы, сохраняющие скалярное произведение ((Ux, Uy) = (x, y)), их аналогом в евклидовых пространствах являются ортогональные операторы.

Def: Линейный оператор P, действующий в евклидовом пространстве называется ортогональным, если "x, yÎV: (Px, Py) = (x, y).

Непосредственно из определения следует, что если {e_k} ортогональный базис в V, то {Pe_k} тоже ортогональный базис в V.

Т°. Чтобы линейный оператор P был ортогональным необходимо и достаточно,

чтобы существовал оператор P^–1 и выполнялось равенство P^* = P^–1.

◀ Необходимость. Пусть P – ортогональный.

(P^*Px, y) = (Px, Py) = (x, y) Þ ((P^*P – Е)x, y) = 0 Þ P^*P = Е Þ (Px, Py) = (x, y) Þ P^* = P^–1.

Достаточность. Пусть P^* = P^–1, (x, y) = (x, P^–1Py) = (x, P^*Py) = (Px, Py) ▶

Def: Матрица называется ортогональной, если P^TP = PP^T = E.

Если е₁, е₂, …, е_n ортонормированный базис в V, то оператор P будет ортогональным тогда и только тогда когда матрица оператора будет ортогональной.

В унитарном пространстве аналогом ортогональной матрицы является унитарная матрица, т.е. такая матрица U, что U^*U = UU^* = E. Здесь U^* эрмитово сопряженная матрица, т. е. 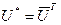. Нетрудно показать, что в ортонормированном базисе матрица линейного оператора U унитарна тогда и только тогда, когда оператор U унитарен.

Рассмотрим ортогональное преобразование в одномерном случае"хÎV₁, x = ae, aÎR, тогда Pe = le Þ (Pe, Pe) = (le, le) = l² (e, e) = (e, e), т.е. l² = 1, l = ±1, таким образом, в одномерном пространстве существует два ортогональных преобразования P₊x = x и P_–x = – x.

Рассмотрим ортогональное преобразование в двумерном случае. Если P задается матрицей 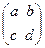, то из условия P^TP = PP^T = E следует, что

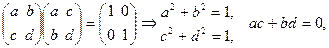
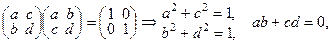
т.е. 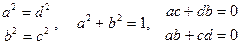. Положив a = cosj, b = – sinj, получим 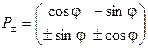, причем во второй строке надо брать либо оба минуса, либо оба плюса. При этом detP_± = ±1.

Ортогональная матрица P₊ называется собственной, а P_- называется несобственной.

В ортонормированном базисе {e₁, e₂} оператор P₊ осуществляет поворот на угол φ в плоскости {e₁, e₂}. Записав P_- = QP₊, где 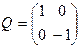, можем сказать, что P_- осуществляет поворот на угол φ в плоскости {e₁, e₂} (P₊), а затем отражение относительно оси e₁ (Q).

В общем случаев n-мерном евклидовом пространстве произвольный ортогональный оператор P в некотором ортонормированном базисе {е₁, е₂, …, е_n} может быть записан в виде:

.

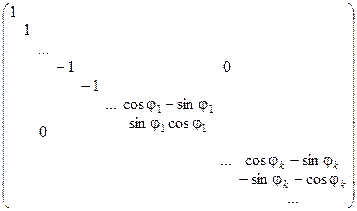Таким образом, в некотором ортонормированном базисе действие ортогонального оператора сводится к последовательным поворотам и отражениям относительно координатных осей.