Форм к сумме квадратов

Т°. Пусть A(x, y) и B(x, y) – симметричные билинейные формы в вещественном

линейном пространстве V. Пусть, кроме того, "xÎV, x ¹ 0, B(x, x) > 0, т.е.

квадратичная форма B(x, x) положительно определена. Тогда в V существует

базис {e_k}, в котором: .

◀ Рассмотрим билинейную форму B(x, y) полярную к квадратичной форме B(x, x). Учитывая свойства B(x, x) в посылке теоремы, форма B(x, y), может задавать скалярное произведение в V (x, y) º B(x, y), теперь V стало евклидовым пространством Þ${e_k} – ортонормированный базис, в котором 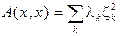, при этом в ортонормированном базисе ▶

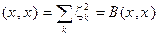Две последние теоремы дают доказательство существования и способ построения канонического базиса квадратичной формы.

Этот способ не более сложен чем, скажем, методы Лагранжа или Якоби, рассмотренные ранее. Однако доказательство полезно тем, что иллюстрирует применение самосопряженных операторов и выглядит здесь достаточно мощно.