Понятие группы. Подгруппы

Множество G элементов x, y, z, … произвольной природы называется группой, если в нем корректно введена внутренняя операция (закон композиции) т.е. "х, yÎG, $zÎG такое, что z = x⊕y или (z = x⊙y), удовлетворяющее условиям:

1) x⊕(y⊕z) = (x⊕y)⊕z ассоциативность 1) x⊙(y⊙z) = (x⊙y)⊙z;

2) $qÎG½"xÎG x⊕q = x нейтральный элемент 2) $еÎG½"xÎG x⊙е = x;

3) 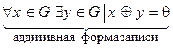обратный элемент 3) .

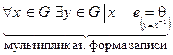Если введенная операция еще и коммутативная, т.е. x⊕y = y⊕x или (x⊙y = y⊙x), то группа называется абелевой.

Подмножество элементов G₁ группы G называется подгруппой, если:

1) "х, уÎG₁ ® x⊙yÎG₁; 2) "хÎG₁ ® x^-1ÎG₁.

(Здесь применена мультипликативная форма записи)

Подгруппа G₁ группы G сама по себе является группой. Простейшими (тривиальными) подгруппами любой группы является сама группа и группа, состоящая из одного элемента – нейтрального.