Еще определения

1°. Если группа конечная – то количество её элементов называют порядком группы.

2°. Группа G из элементов а⁰ = е, а, а², а³, …, а^k = е называется циклической группой, порождаемой элементом а. Порядок группы – ½G½= k.

3°. Группа поворотов правильного многоугольника относительно его центра является циклической группой n^го порядка. Порождается элементом P_2π/n (поворот на угол 2π/n против часовой стрелки). Эта группа обозначается C_n.

4°. Группа целых чисел по сложению также циклическая, ибо порождается одним элементом (0, 1, 1 + 1, 1 + 1 + 1, …, –(1), –(1 + 1), …), Группа обозначается С_¥.

5°.ЕслиН₁ и Н₂ помножества группы G, то Н 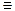{h ½ h=h₁+h₂, h₁ G₁ , h₂ G₂} называется суммой двух подмножеств группы G и обозначается G₁ + G₂ . Если, при этом, представление h=h₁+h₂ единственно, то сумма подмножеств называется прямой суммой и обозначается Н₁ Å Н₂ . Отметим что, сумма двух подгрупп группы подгруппой, вообще говоря, не является. ( Попробуйте привести пример )

6°. Т°.G=G₁ÅG₂Å…ÅG_k Û (G₁,g₂,…G_i-1)ÇG_i={q}, "i£k.

Для того чтобы группу G можно было представить в виде прямой суммы подгрупп G₁,G₂,…,G_k необходимо и достаточно, чтобы подгруппы не имели других общих элементов, кроме нейтрального.

Т°.Пусть½G½= nи n=k×l.НОД(k, l) = 1. Тогда $G_k,G_l Ì G, ½G_k½=k, ½G_l½=l : G=G_kÅG_l (для абелевых циклических групп).

7°.Если для циклической группы G порядок группы ½G½=pⁿ (n>1), где p – простое число, то группа называется примарной.

Т°.Примарная группа не может быть разложена в прямую сумму нетривиальных подгрупп.

8°. Т°(Лагранжа).Если G₁ - подгруппа конечной группы G то порядок подгруппы G₁ является делителем порядка группы G.