Смежные классы. Нормальные делители

Если H₁ и H₂ – подмножества группы G, то произведением H₃ подмножеств H₁ и H₂ называется H₃ = H₁×H₂ º {h₃½h₃ = h₁×h₂; h₁ÎH₁; h₂ÎH₂}.

Отметим, что если H₁ и H₂ – подгруппы группы G, то H₁×H₂, вообще говоря, не подгруппа.

◀ В самом деле, если 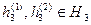, то

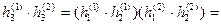
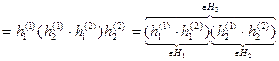, если бы можно было, то …. Но коммутативный закон, вообще говоря, не выполнен ▶

Если H подгруппа G и aÎG, то aH и Ha, рассматриваемые как произведения множества Н и одноэлементного множества {a}, называются левым и правым смежными классами подгруппы Н в G. Изменение а влечет за собой, вообще говоря, изменение смежных классов.

§7. Свойства смежных классов (сформулированы для левых,

но справедливы и для правых)

1°. aÎH Þ aH º H. Доказать самостоятельно.

2°. a^-1bÎH Þ aH = bH. ◀ a^-1bH º H (из 1°) и тогда bH = (aa^-1)bH = a(a^-1bH) = aH ▶

3°. Два смежных класса одной подгруппы H либо совпадают, либо не имеют общих элементов.

◀ Пусть аН и bH имеют общий элемент, т.е. для h₁, h₂ÎH, ah₁ = bh₂ Þ a^-1b = 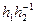ÎH и т.к. 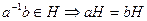(из 2°) ▶

4°. aÎaH. Доказать самостоятельно.

Пусть Н такая подгруппа G для которой все левые смежные классы являются и правыми смежными классами. В этом случае, аН = На, "aÎG. Подгруппа Н для которой все левые смежные классы являются одновременно и правыми смежными классами называется нормальным делителем группы G.

Т°. Если Н – нормальный делитель группы G, то произведение смежных классов –

смежный класс.

◀ аН, bН – смежные классы, аН×bН = a(Н×b)H = a(bH)H = (ab)H×H = (ab)H ▶