Изоморфизм групп

Две группы G₁ и G₂ называются изоморфными, если существует взаимно однозначное соответствие f между элементами G₁ и G₂: 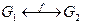такое, что если .

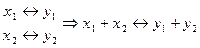Для изоморфных групп: e₁ « e₂, a, a^-1 « f(a), f(a^-1). Изоморфные группы с точки зрения групповых свойств неразличимы.

Примеры изоморфных групп:

а) группа самосовмещений равностороннего треугольника и группа перестановок из трех элементов.

б) Группа вычетов по модулю 2: Z₂ и группа, состоящая из двух преобразований евклидового пространства: тождественного преобразования и отражения относительно θ.

Изоморфное отображение группы G на саму себя называется автоморфизмом. Если отдельные автоморфизмы группы рассматривать как некоторые элементы, а последовательное проведение автоморфизмов, как произведение соответствующих элементов, то автоморфизмы сами по себе образуют группу, единичным элементом которой является тождественный автоморфизм. Эта группа называется группой автоморфизмов данной группы G.