Примеры построения смежных классов

1°. Рассмотрим группу S₃ (группа перестановок 3^х элементов).

Левые смежные классы группы S₃ по подгруппе B = {P₁, P₂} состоит из классов:

B; P₅B = P₄B = {P₄, P₅}; P₃B = P₆B = {P₃, P₆}.

Правые смежные классы группы S₃ по подгруппе B = {P₁, P₂} состоит из классов:

B; BP₆ = BP₄ = {P₄, P₆}; BP₅ = BP₃ = {P₃, P₅}.

Здесь множество левых и правых смежных классов не совпадают.

Однако … левые и правые смежные классы группы S₃ по подгруппе A = {P₁, P₅, P₆} совпадают: A; AP₂ = P₂A = {P₂, P₃, P₄}.

В данном случае подгруппа А – есть нормальный делитель группы S₃.

2°. В множестве целых чисел Z рассмотрим аддитивную подгруппу чисел, делящихся на пять: A₅ = {…, –10, –5, 0, 5, 10, …}.

Левые и правые смежные классы здесь такие, 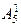{…, –9, –4, 1, 6, 11, …} – множество чисел, которые при делении на пять дают в остатке единицу. Аналогично 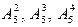– множества чисел, которые при делении на пять, дают в остатке 2, 3, 4 соответственно.

Все левые смежные классы совпадают с правыми смежными классами. Таким образом, A₅ – нормальный делитель группы Z. Если обозначить B₅ множество целых чисел, не делящихся на пять, то можно записать Z = A₅´В₅, где знак обозначает прямое произведение.

Замечание: Множество классов 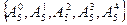образую аддитивную группу с нейтральным элементом .

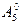Эта группа называется фактор-группой группы Z по подгруппе A₅ и обозначается Z/A₅.