Группы линейных преобразований

1°. Рассмотрим множество невырожденных линейных операторов (преобразований), действующих из V_n в V_n. Если определить произведение линейных операторов по правилу (AB)x = A(Bx), то:

Тº. Множество GL(n) невырожденных линейных преобразований линейного n-мерного пространства V с операцией умножения операторов введенной,как (АВ)х = А(Вх) представляет собой группу.

Эта группа называется группой линейных невырожденных преобразований линейного пространства V_n и обозначается: GL(n).

2°. Короткое воспоминание: Линейный оператор Р в евклидовом пространстве называется ортогональным, если "x, yÎV (евклидово пространство) (Px, Py) = (x, y).

Условие ортогональности оператора: Оператор Р₂ ортогонален тогда и только тогда когда существует Р^-1 и Р^-1 = Р^*.

Тº. Множество всех ортогональных операторов евклидового пространства V_n с

обычной операцией умножения линейных операторов образует группу.

Эта группа называется ортогональной группой и обозначается О(n).

◀ Пусть Р₁ и Р₂ – ортогональные операторы. Докажем, что Р₁Р₂ тоже ортогональный оператор (Р₁Р₂x, Р₁Р₂x) 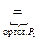(Р₂x, Р₂x) (x, y) ▶

3°. Еще воспоминание: Если оператор Р ортогонален, то detP = ±1. Поэтому все ортогональные операторы Р делятся на два класса:

а) Р для которых detP = 1 (эти преобразования называются собственными)

б) Р для которых detP = -1 (эти преобразования называются несобственными)

Тº. Множество всех собственных ортогональных преобразований образует группу, которая называется собственной ортогональной группой и обозначается SO(n).

4°. O(n) есть подгруппа GL(n); SO(n) есть подгруппа О(n).

5°. В комплексном линейном пространстве также можно рассмотреть группу линейных преобразований. Если в комплексном пространстве со скалярным произведением (унитарное пространство) рассмотреть множество линейных операторов, сохраняющих скалярное произведение: (U_x, U_y) = (x, y) (такие операторы называются унитарными), то окажется, что унитарные операторы образуют группу. Эта группа называется унитарной группой, обозначается U_n и является аналогом ортогональной группы в унитарном пространстве.