В ЛИНЕЙНЫХ ЦЕПЯХ
4.1. Гармонические ток и напряжение в элементах цепи
В элементах цепи R, L, и C взаимосвязь произвольных мгновенных значений тока и напряжения определяется законом Ома, необходимые соотношения приведены в табл. 1.1.
 Рассмотрим гармонические ток и напряжение на элементе Э (рис. 4.1) в виде
Рассмотрим гармонические ток и напряжение на элементе Э (рис. 4.1) в виде
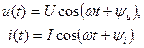 (4.1)
(4.1)
Рис. 4.1
Для сопротивления R можно записать
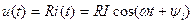 . (4.2)
. (4.2)
Сравнивая полученный результат с выражением для напряжения из (4.1), получим выражение закона Ома для амплитуд тока и напряжения.
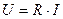 , (4.3)
, (4.3)
и соотношение для начальных фаз
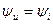 . (4.4)
. (4.4)
Как видно из (4.3), амплитуды (и действующие значения) гармонических тока и напряжения в сопротивлении связаны законом Ома в классической формулировке прямой пропорциональности.
Начальные фазы тока 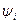 и напряжения
и напряжения 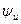 в сопротивлении одинаковы, сдвиг фаз
в сопротивлении одинаковы, сдвиг фаз 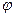 между напряжением и током равен нулю,
между напряжением и током равен нулю,
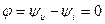 . (4.5)
. (4.5)
Мгновенная мощность (1.6) гармонических сигналов в сопротивлении равна
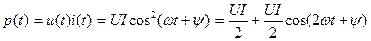 , (4.6)
, (4.6)

где 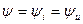 . Ее зависимость от времени показана на рис. 4.2. Величина
. Ее зависимость от времени показана на рис. 4.2. Величина 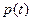 всегда положительна, то есть сопротивление только потребляет мощность от источника сигнала. Это гармоническая функция времени с периодом по-
всегда положительна, то есть сопротивление только потребляет мощность от источника сигнала. Это гармоническая функция времени с периодом по-
вторения в два раза меньше пе- Рис. 4.2
риода сигнала.
Средняя мощность (1.8) гармонических сигналов в сопротивлении определяется выражением
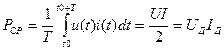 , (4.7)
, (4.7)
где 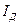 и
и 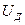 - действующие значения тока и напряжения,
- действующие значения тока и напряжения,
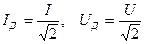 . (4.8)
. (4.8)
Это значение показано пунктирной линией на временной диаграмме рис. 4.2.
В емкости C мгновенные значения тока и напряжения связаны соотношением (табл.1.1)
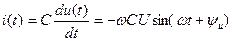 . (4.9)
. (4.9)
После преобразования тригонометрической функции к канонической форме гармонического сигнала получим
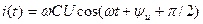 . (4.10)
. (4.10)
Сравнивая (4.10) с формулой тока из (4.1), можно записать
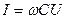 , (4.11)
, (4.11)
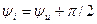 . (4.12)
. (4.12)
Введем обозначения
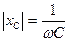 , (4.13)
, (4.13)
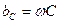 , (4.14)
, (4.14)
где 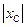 - модуль реактивного сопротивления емкости (Ом), а
- модуль реактивного сопротивления емкости (Ом), а 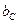 - реактивная проводимость емкости (См=1/Ом). Позднее увидим, что реактивное сопротивление емкости отрицательно.
- реактивная проводимость емкости (См=1/Ом). Позднее увидим, что реактивное сопротивление емкости отрицательно.
Из (4.11) получим уравнения связи амплитуд (и действующих значений) гармонических тока и напряжения в емкости
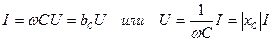 , (4.15)
, (4.15)
которые представляют собой выражение закона Ома для емкости в классической формулировке прямой пропорциональности.
Из (4.12) следует, что гармонический ток в емкости опережает по фазе приложенное к ней напряжение (напряжение отстает по фазе от тока) на угол 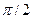 радиан или 900. Сдвиг фаз между напряжением и током в емкости равен
радиан или 900. Сдвиг фаз между напряжением и током в емкости равен

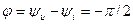 . (4.16)
. (4.16)
На рис. 4.3 показаны временные диаграммы тока и напряжения в емкости. Ток 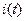 опережает по фазе напряжение на 900, что отражается на временной диаграмме смещением
опережает по фазе напряжение на 900, что отражается на временной диаграмме смещением
кривой тока влево на чет- Рис. 4.3
верть периода.
Мгновенная мощность в емкости из (4.1) и (4.9) равна
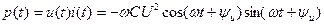 ,
,
а после тригонометрических преобразований получим
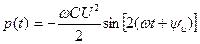 . (4.17)
. (4.17)
Временная диаграмма мгновенной мощности показана на рис. 4.4
 Мгновенная мощность электрических сигналов в емкости может быть положительной (емкость накапливает энергию электрического поля) и отрицательной (емкость отдает во внешнюю цепь ранее накопленную энергию). Средняя мощность гармонических
Мгновенная мощность электрических сигналов в емкости может быть положительной (емкость накапливает энергию электрического поля) и отрицательной (емкость отдает во внешнюю цепь ранее накопленную энергию). Средняя мощность гармонических
сигналов в емкости равна нулю, то
Рис. 4.4 есть емкость не потребляет мощ-
ность от гармонического источника.
Для индуктивности L мгновенные значения тока и напряжения связаны соотношением закона Ома из табл.1.1, тогда с учетом выражения для тока из (4.1) получим
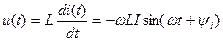 ,
,
а после преобразований
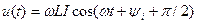 . (4.18)
. (4.18)
Сравнивая (4.18) с выражением для напряжения (4.1), получим уравнения связи для амплитуд (действующих значений) тока и напряжения
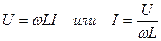 (4.19)
(4.19)
и их начальных фаз
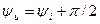 . (4.20)
. (4.20)
Введем обозначения
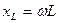 , (4.21)
, (4.21)
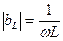 , (4.22)
, (4.22)
где 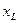 - реактивное сопротивление индуктивности (Ом), а
- реактивное сопротивление индуктивности (Ом), а 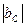 - модуль реактивной проводимости индуктивности (См=1/Ом). Позднее увидим, что реактивная проводимость индуктивности отрицательна.
- модуль реактивной проводимости индуктивности (См=1/Ом). Позднее увидим, что реактивная проводимость индуктивности отрицательна.
Тогда получим выражения закона Ома для амплитуд (действующих значений) тока и напряжения в индуктивности
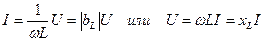 . (4.23)
. (4.23)
Согласно (4.20) гармонический ток в индуктивности отстает по фазе от напряжения (напряжение опережает по фазе ток) на угол 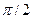 радиан или 900. Сдвиг фаз между напряжением и током в индуктивности равен
радиан или 900. Сдвиг фаз между напряжением и током в индуктивности равен

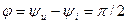 . (4.24)
. (4.24)
Временные диаграммы тока и напряжения в индуктивности показаны на рис. 4.5. В отличие от аналогичных графиков для емкости на рис. 4.3 ток и напряжение меняются
местами, кривая напряже- Рис. 4.5
ния смещена вправо отно-
сительно тока на четверть периода, что соответствует опережению по фазе на 900.
Мгновенная мощность гармонических сигналов в индуктивности равна
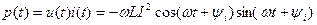 , (4.25)
, (4.25)
а после тригонометрических преобразований получим
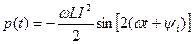 . (4.26)
. (4.26)
Временная диаграмма мгновенной мощности в индуктивности совпадает с показанной на рис. 4.4 для емкости.
Средняя мощность гармонических сигналов в индуктивности (как и в емкости) равна нулю, то есть индуктивность не потребляет мощность от гармонического источника.
В табл. 4.1 приведены сводные результаты для гармонических сигналов в элементах цепи.
Таблица 4.1
| Элемент | Ток | Напряжение | Средняя мощность |
| R | 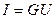
| 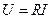
| 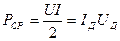
|
| C | 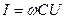
| 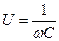
| 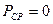
|
| L |  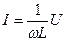
| 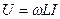
| 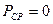
|
4.2. Средняя мощность гармонических сигналов в
линейном двухполюснике
Рассмотрим двухполюсник (ДП) на рис. 4.6, через который протекает гармонический ток 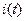 и к которому приложе-
и к которому приложе-
но напряжение 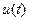 вила (4.1).
вила (4.1).
 Мгновенная мощность равна
Мгновенная мощность равна
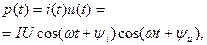 (4.27)
(4.27)
а после тригонометрических преобра- Рис.4.6
зований получим
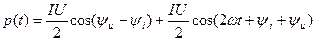 . (4.28)
. (4.28)
Как видно, мгновенная мощность изменяется по гармоническому закону с частотой 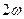 и содержит постоянную составляющую.
и содержит постоянную составляющую.
Средняя мощность равна
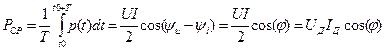 , (4.29)
, (4.29)
где 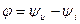 - сдвиг фаз между напряжением и током. Величину
- сдвиг фаз между напряжением и током. Величину 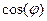 называют коэффициентом мощности.
называют коэффициентом мощности.
Как видно, потребляемая двухполюсником мощность определяется амплитудами (действующими значениями) тока и напряжения и коэффициентом мощности. Для максимизации потребляемой мощности (например, электродвигателем) необходимо обеспечить условие 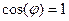 , то есть нулевой сдвиг фаз между напряжением и током (
, то есть нулевой сдвиг фаз между напряжением и током ( 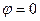 ). Это означает, что двухполюсник должен вести себя как сопротивление
). Это означает, что двухполюсник должен вести себя как сопротивление 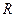 .
.
В чисто реактивной цепи, содержащей только индуктивности и емкости, сдвиг фаз 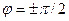 , при этом потребляемая мощность будет рана нулю при любых амплитудах тока и
, при этом потребляемая мощность будет рана нулю при любых амплитудах тока и
напряжения.
Полученное выражение (4.29) для средней мощности полностью согласуется со значениями 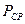 в элементах цепи R, L и C (табл. 4.1), так как в сопротивлении
в элементах цепи R, L и C (табл. 4.1), так как в сопротивлении 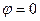 , а в индуктивности и емкости
, а в индуктивности и емкости 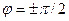 .
.

4.3. Тригонометрический метод расчета
Тригонометрический метод расчета гармонических токов и напряжений в линейной цепи базируется на законах Ома и Кирхгофа для мгновенных значений сигналов в тригонометрической форме.
 В качестве примера рассмотрим цепь на рис. 4.7 при
В качестве примера рассмотрим цепь на рис. 4.7 при 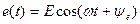 ,
, 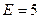 В,
В, 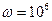 рад/с,
рад/с, 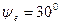 ,
, 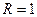 кОм и
кОм и 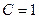 нФ. Обозначим гармонический ток
нФ. Обозначим гармонический ток 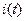 в виде
в виде
Рис. 4.7
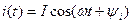 , (4.30)
, (4.30)
тогда с учетом свойств гармонических напряжений в сопротивлении и емкости на основе второго закона Кирхгофа получим
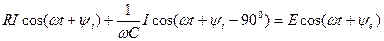 . (4.31)
. (4.31)
Левая часть (4.31) может быть преобразована в тригонометрическую функцию,
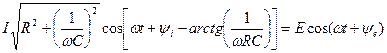 , (4.32)
, (4.32)
тогда, уравнивая коэффициенты в правой и левой частях уравнения, получим
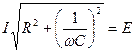 , (4.33)
, (4.33)
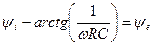 . (4.34)
. (4.34)
Из полученных выражений нетрудно определить амплитуду и начальную фазу тока в цепи,
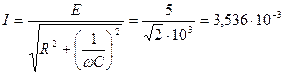 А,
А,
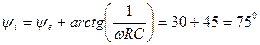 .
.
При найденном токе нетрудно определить напряжение 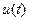 на емкости (проведите расчет самостоятельно).
на емкости (проведите расчет самостоятельно).
Как видно, тригонометрический метод требует суммирования гармонических функций с неизвестными параметрами, что приводит к громоздким расчетам, если число слагаемых функций более двух. Этот метод применим для расчета
очень простых цепей.
4.4. Векторная диаграмма цепи
 Гармонический сигнал
Гармонический сигнал 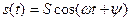 можно представить проекцией на горизонтальную ось вектора, вращающегося против часовой стрелки вокруг начала координат с круговой (угловой) частотой
можно представить проекцией на горизонтальную ось вектора, вращающегося против часовой стрелки вокруг начала координат с круговой (угловой) частотой 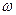 , как показано на рис. 4.8. Длина (модуль) вектора равна амплитуде гармонического сигнала
, как показано на рис. 4.8. Длина (модуль) вектора равна амплитуде гармонического сигнала 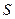 и в момент начала вращения (при
и в момент начала вращения (при 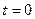 ) угол его наклона к горизонтальной
) угол его наклона к горизонтальной
Рис. 4.8 оси равен начальной фазе сиг-
нала 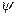 (отсчет положительных значений проводится против часовой стрелки).
(отсчет положительных значений проводится против часовой стрелки).
Все гармонические токи и напряжения в цепи с одинаковой частотой, равной частоте источников сигнала, можно представить совокупностью синхронно вращающихся векторов вида рис. 4.8. Так как все векторы вращаются синхронно и между ними сохраняются амплитудные и угловые соотношения, то вращение можно остановить и рассматривать неподвижную совокупность векторов. Если вращение остановлено в момент времени 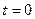 , то угол наклона каждого вектора к горизонтальной оси равен начальной фазе соответствующего вектору гармонического сигнала.
, то угол наклона каждого вектора к горизонтальной оси равен начальной фазе соответствующего вектору гармонического сигнала.

Для векторного представления гармонических сигналов выполняются законы Кирхгофа в классической формулировке.
В качестве примера рассмотрим векторную диаграмму цепи, показанной на рис. 4.7. Результаты ее расчета тригонометрическим методом приведены в табл. 4.2 (проведите соответствующие расчеты).
Таблица 4.2
| Сигнал | Амплитуда | Начальная фаза |
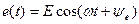
| 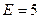 В В
| 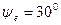
|
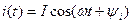
| 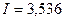 мА мА
| 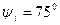
|
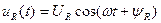
| 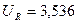 В В
| 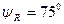
|
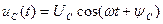
| 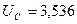 В В
| 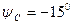
|
 Векторная диаграмма цепи приведена на рис. 4.9. Векторы тока и напряжений построены по данным табл. 4.2, длина вектора равна амплитуде сигнала, а угол отклонения от горизонтальной оси равен начальной фазе (отсчет положительных значений угла против часовой стрелки). Вектор тока
Векторная диаграмма цепи приведена на рис. 4.9. Векторы тока и напряжений построены по данным табл. 4.2, длина вектора равна амплитуде сигнала, а угол отклонения от горизонтальной оси равен начальной фазе (отсчет положительных значений угла против часовой стрелки). Вектор тока 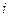 совпадает по направлению с вектором напряжения
совпадает по направлению с вектором напряжения 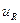 на сопротивлении, их длины (модули)
на сопротивлении, их длины (модули)
не одинаковы, так как масштабы Рис. 4.9
штабы (например, В/см и мА/см)
токов и напряжений различны (ток и напряжение не сравнимы между собой).
Напряжение на сопротивлении 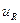 опережает по фазе напряжение на емкости
опережает по фазе напряжение на емкости 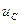 на 900. Это обусловлено тем, что в
на 900. Это обусловлено тем, что в
последовательной цепи рис. 4.7 через сопротивление и емкость протекает один и тот же ток, причем напряжение на сопротивлении совпадает по фазе с током, а на емкости – отстает по фазе от тока на 900.
Сумма векторов напряжений на сопротивлении и емкости в цепи рис. 4.7 по второму закону Кирхгофа (в векторной форме) равна ЭДС источника, что и показано на векторной диаграмме рис. 4.9.
Как видно, векторная диаграмма цепи может быть построена по результатам расчета всех гармонических токов и напряжений. Однако ее можно построить «качественно» (без знания точных параметров векторов, но с правильными соотношениями между ними) и не проводя численных расчетов.
 Рассмотрим пример RC цепи, показанной на рис. 4.10, в которой заданы положительные направления и условные обозначения всех токов и напряжений.
Рассмотрим пример RC цепи, показанной на рис. 4.10, в которой заданы положительные направления и условные обозначения всех токов и напряжений.
Прежде всего, необходимо проанализировать структуру цепи. В ней присутствует
Рис. 4.10 параллельный фрагмент (со-
единение элементов C и R2), который соединен последовательно с сопротивлением R1 и источником напряжения 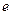 . Тогда построение необходимо начать с напряжения на параллельном фрагменте, при этом
. Тогда построение необходимо начать с напряжения на параллельном фрагменте, при этом 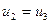 , этот вектор проведем произвольно по модулю и направлению, например, горизонтально, векторная диаграмма показана на рис. 4.11.
, этот вектор проведем произвольно по модулю и направлению, например, горизонтально, векторная диаграмма показана на рис. 4.11.
Ток 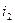 совпадает по фазе с напряжениями
совпадает по фазе с напряжениями 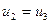 , а ток
, а ток 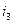 опережает их по фазе на 900. Соответствующие векторы изображены на диаграмме рис. 4.11 с произвольной длиной и указанными угловыми соотношениями относительно вектора
опережает их по фазе на 900. Соответствующие векторы изображены на диаграмме рис. 4.11 с произвольной длиной и указанными угловыми соотношениями относительно вектора

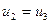 . Векторная сумма этих токов по первому закону Кирхгофа равна току
. Векторная сумма этих токов по первому закону Кирхгофа равна току 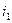 , то есть этот вектор строится исходя из векторов
, то есть этот вектор строится исходя из векторов 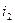 и
и 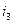 . Вектор напряжения
. Вектор напряжения 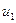 на сопротивлении R1 совпадает по направлению с вектором тока
на сопротивлении R1 совпадает по направлению с вектором тока 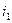 и имеет произвольную длину, а вектор ЭДС
и имеет произвольную длину, а вектор ЭДС 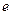 по второму закону Кирхгофа Кирхгофа равен Рис. 4.11
по второму закону Кирхгофа Кирхгофа равен Рис. 4.11
сумме векторов 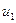 и
и
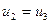 . На этом построение «качественной» векторной диаграммы цепи заканчивается.
. На этом построение «качественной» векторной диаграммы цепи заканчивается.
Если цепь содержит последовательный фрагмент, входящий в смешанное соединение, то построение целесообразно начинать с вектора тока этого фрагмента.
Векторная диаграмма электрической цепи может использоваться для иллюстрации амплитудных и фазовых соотношений между токами и напряжениями, и для формирования аналитических выражений, связывающих их амплитуды (действующие значения) и начальные фазы.
Например, для диаграммы рис. 4.11 амплитуды (действующие значения) токов 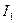 ,
, 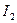 и
и 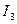 по теореме Пифагора связаны выражением
по теореме Пифагора связаны выражением 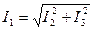 . Для других соотношений можно использовать теорему косинусов (пример приведите самостоятельно).
. Для других соотношений можно использовать теорему косинусов (пример приведите самостоятельно).
Для сложной цепи построение «качественной» векторной диаграммы требует вдумчивого подхода при выборе начального вектора и способов построения остальных векторов.
4.5. Особенности расчета цепи с гармоническими
сигналами
Мгновенные значения токов и напряжений в электрической цепи связаны между собой уравнениями законов Ома и Кирхгофа. Последние предполагают суммирование гармонических функций времени с неизвестными амплитудами и начальными фазами, например, с помощью теоремы косинусов, а это приводит к громоздким расчетам даже в относительно простых цепях.
Существенно упростить расчеты можно, отказавшись от описания сигналов с помощью тригонометрических функций времени и заменив его числами, на зависящими от времени. На эту возможность указывает векторная диаграмма цепи, которая полностью отражает свойства гармонических сигналов и не зависит от времени.
Известно, что вектор, выходящий из начала координат, можно представить комплексным числом. Таким образом, в теории электрических цепей при расчете гармонических процессов возникает метод комплексных амплитуд.
4.6. Расчет средней (потребляемой) мощности
По результатам расчета гармонических токов и напряжений можно определить мощность, потребляемую цепью от источника сигнала.
В качестве примера используем цепь на рис. 4.7, результаты расчета приведены в табл. 4.2. Рассматривая цепь относительно зажимов источника как двухполюсник, при амплитуде напряжения 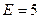 В, тока
В, тока 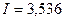 мА и сдвиге фаз между ними
мА и сдвиге фаз между ними 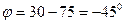 , получим
, получим
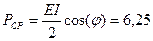 мВт.
мВт.
С другой стороны, в рассматриваемой цепи емкость не потребляет мощность гармонического сигнала, и она может выделяться только в сопротивлении. Тогда получим
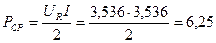 мВт.
мВт.
Как видно результаты совпадают.
Если в цепи имеется несколько сопротивлений, то общая потребляемая цепью мощность будет равна сумме мощностей, потребляемых каждым сопротивлением в отдельности.
4.7. Задания для самостоятельного решения
Задание 4.1.Тригонометрическим методом определите амплитуды и начальные фазы токов и напряжений на элементах цепей, показанных на рис. 4.12, при 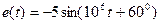 В,
В, 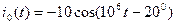 мА,
мА, 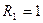 кОм,
кОм, 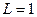 мГн и
мГн и 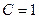 нФ.
нФ.
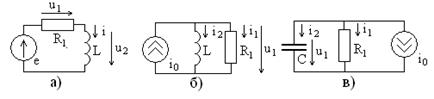
Рис. 4.12
По результатам расчета постройте полные векторные диаграммы цепей, проверьте выполнимость законов Кирхгофа.
Задание 4.2. Постройте «качественные» векторные диаграммы цепей, показанных на рис. 4.12. Сравните их с расчетными диаграммами из задания 4.1.
Задание 4.3. Определите мощность, потребляемую от источника сигнала в цепях, показанных на рис. 4.12. Проведите расчеты, рассматривая цепь как двухполюсник или выделив в ней энергопотребляющие элементы.
Задание 4.4. Постройте «качественные» полные векторные диаграммы цепей, показанных на рис. 4.13.
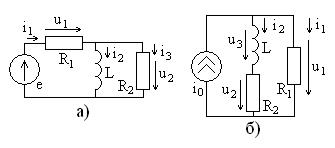
Рис. 4.13
Задание 4.5. Тригонометрическим методом определите амплитуды и начальные фазы токов и напряжений на элементах цепи, показанной на рис. 4.10, при 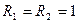 кОм,
кОм, 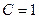 нФ и
нФ и 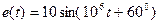 В.
В.
Постройте полную векторную диаграмму цепи, сравните ее с приведенной на рис. 4.11. Определите мощность, потребляемую цепью от источника.
Дата добавления: 2015-06-17; просмотров: 1765;
