Виды нелинейных регрессионных моделей, расчет их параметров

Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.

В случае, когда между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.

Различает две группы нелинейных регрессионных моделей:

­ модели, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

­ модели нелинейные по оцениваемым параметрам.

К первой группе относятся, например, следующие виды функций:

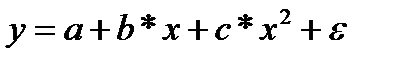- полином 2-й степени;

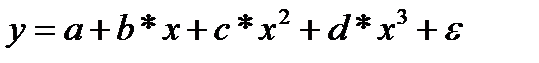- полином 3-й степени;

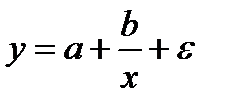- гипербола.

Ко второй группе относятся:

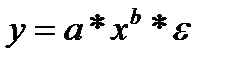- степенная;

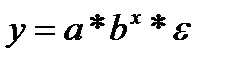- показательная;

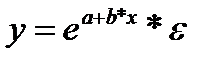- экспоненциальная

и др. виды функций.

Классическим примером функций, относящихся к первой группе, являются кривые Филипса и Энгеля:

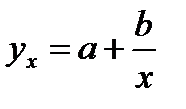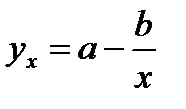и , соответственно.

Первая функция характеризует нелинейные соотношения между нормой безработицы x и процентом прироста заработной платы у. Из данной зависимости следует, что с ростом уровня безработицы темпы роста заработной платы в пределе стремится к нулю.

Вторая функция устанавливает закономерность – с ростом дохода доля расходов на продовольствие - уменьшается. Здесь у, обозначает - долю расходов на непродовольственные товары; х – доходы.

Первая группа нелинейных функций легко может быть линеаризована (приведены к линейному виду). Например, для полинома к-го порядка

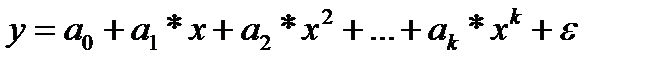производя замену:

х=х₁, х²=х₂, х³=х₃,…,х^к=х_к получим линейную модель вида

.

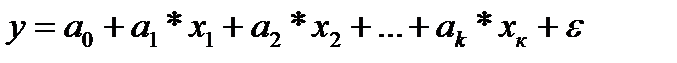32. Модели регрессии, нелинейные по оцениваемым коэффициентам

Модели регрессии, нелинейные по оцениваемым коэффициентам могут быть линеаризованы путем соответствующих замен.

Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций.

Иначе обстоит дело с группой регрессионных, нелинейных функций по оцениваемым параметрам. Данную группу функций можно разбить на две подгруппы:

­ нелинейные модели внутренне линейные;

­ нелинейные модели внутренне нелинейные.

Рассмотрим степенную функцию 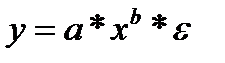. Она нелинейна относительно параметров а и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:

ln y =ln a+b*ln x +ln ε .

Следовательно, ее параметры могут быть найдены обычным МНК.

Если модель представить в виде:

y = a *x^b +ε , то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.

Внутренне нелинейной будет и модель вида

y = a *b *x^c +ε

В эконометрических исследованиях, часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые легко преобразуются в линейный вид, относятся к группе линейных моделей. Например, к линейным относят модель:

y = e^a+bx *ε , так как

ln y =a+b*x+ln ε .

Если, модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные методы, успешность которых зависит от вида функции и особенностей применяемого итеративного подхода.

МНК в случае нелинейных функций, рассмотрим на примере оценки параметров степенной функции y =a*x^b*ε.

Прологарифмировав данную функцию, получим:

ln y =ln a+b *ln x + ln ε или, производя обозначения:

y₁ =a₁+b*x₁+ε. , где

y₁ = ln y ; a₁= ln a; x₁ =ln x; ε = ln ε.

Применив МНК к полученному уравнению:

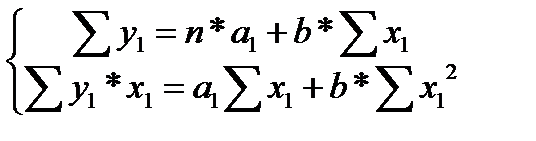, или

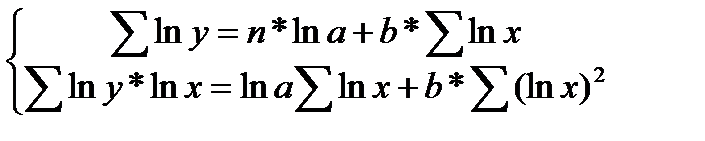
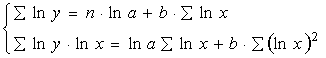
Параметр b определяется непосредственно из системы, а параметр а – косвенным путем: a=e^a1

33. Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным

Применение МНК для оценки параметров моделей регрессии, нелинейных по факторным переменным рассмотрим на примере параболы второй степени. При метод МНК видоизменяет первоначальные уравнения и приводит их к следующей системе нормальных уравнений:

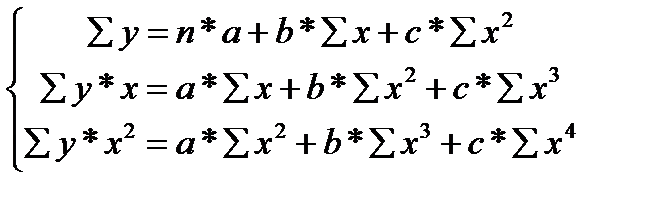(36.1)

Решить данную систему относительно параметров а, b, с можно методом определителей:

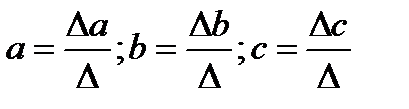(36.2)

где Δ — определитель системы;

Δа, Δb, Δс — частные определители для каждого из параметров.

При b > О и с <0 кривая симметрична относительно высшей точки, т., е. точки перелома кривой, изменяющей направление связи, а именно рост на падение. Такую функцию можно наблюдать в социальной сфере семейных отношений – при взрослении ребенка (с 7-10 лет) увеличиваются его карманные расходы, выдаваемые родителями. Однако, при достижении ребенком определенного возраста (22-25лет) и обретении им самостоятельности потребность в «родительских» карманных средствах перестает существовать. Если параболическая форма связи демонстрирует сначала рост, а затем снижение уровня значений результативного признака, то определяется значение фактора, при котором достигается максимум.

Ввиду симметричности кривой параболу второй степени не всегда можно использовать в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной.

34 Метод наименьших квадратов для моделей регрессии, нелинейных по оцениваемым коэффициентам

Метод наименьших квадратов для моделей регрессии, нелинейных по оцениваемым коэффициентам рассмотрим на примере кривой Филипса, определяющая нелинейное отношение между нормативами безработицы и относительными изменениями зарплаты.

Если в уравнении равносторонней гиперболы 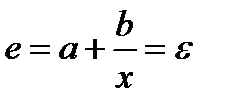(37.1)

заменить 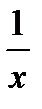на z, получим линейное уравнение регрессии

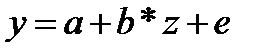(37.2)

оценка параметров которого может быть дана МНК. Система нормальных уравнений имеет вид: 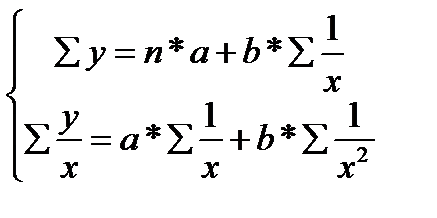(37.3)

При b >0 имеем обратную зависимость, которая при х → ∞ характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр а.

При b <0 имеем медленно повышающуюся Функцию с верх ней асимптотой при х → ∞, т. е. с максимальным предельным уровнем у, оценку которого в уравнении 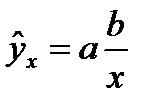дает параметр а.

В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразо­ванным уравнениям. Если в линейной модели и моделях, нели­нейных по переменным, при оценке параметров исходят из кри­терия 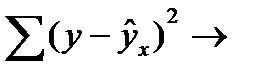min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным дан­ным результативного признака, а к их преобразованным величи­нам, т. е.ln y, 1/y. Так, в степенной функции 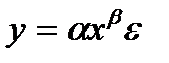МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на миними­зации суммы квадратов отклонений в логарифмах. 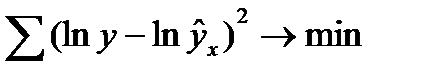(37.4)

Соответственно если в линейных моделях 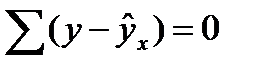то в моделях, нелинейных по оцениваемым параметрам,

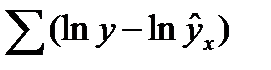. (37.5)

Вследствие этого оценка параметров оказываются несколько смещенной.

35. Дополнительные методы нелинейного оценивания коэффициентов модели регрессии(матрица Гессе, метод Хука-Дживиса, Розенброка).

Матрица Гессе и стандартные ошибки. Матрицу частных производных второго порядка также часто называют матрицей Гессе. Оказывается, что обратная к ней матрица приблизительно равна матрице ковариаций оцениваемых параметров. Интуитивно понятно, что существует обратная зависимость между производными второго порядка по параметрам и их стандартными ошибками. Если изменить угловой коэффициент в точке минимума функции и сделать минимум функции более “резким”, то производные второго порядка увеличатся; при этом, оценки параметров будут практически стабильными в смысле, что параметры в точке минимума будут легко уточняемы. Если же производная второго порядка будет близка к нулю, то угол наклона в точке минимума будет практически неизменным, приводя к тому, что вы можете двигать параметры практически в любом направлении почти не изменяя значение функции потерь. Поэтому стандартные ошибки параметров будут очень большими.

Матрица Гессе и асимптотические стандартные ошибки для параметров вычисляются отдельно методом конечных разностей. Эта процедура возвращает очень точные асимптотические стандартные ошибки для всех методов оценивания.

Метод Хука-Дживиса. В некотором смысле, это простейший из всех алгоритмов. При каждой итерации метод сначала определяет схему расположения параметров, оптимизируя текущую функцию потерь перемещением каждого параметра по отдельности. При этом вся комбинация параметров сдвигается на новое место. Это новое положение в m-мерном пространстве параметров определяется экстраполяцией вдоль линии, соединяющей текущую базовую точку с новой точкой. Размер шага этого процесса постоянно меняется для попадания в оптимальную точку. Этот метод обычно очень эффективен и его следует использовать, если квази-ньютоновский и симплекс-метод (см. выше) не дали удовлетворительных оценок.
Метод Розенброка. Даже если все остальные методы не сработали, метод Розенброка часто приводит к правильному результату. Этот метод вращает пространство параметров, располагая одну ось вдоль “гребня” поверхности (этот метод также называется метод вращения координат), при этом все другие остаются ортогональными выбранной оси. Если поверхность графика функции потерь имеет одну вершину и различимые “гребни” в направлении минимума функции потерь, этот метод приводит к очень точным значениям параметров, минимизирующим функцию потерь. Однако следует отметить, что этот поисковый алгоритм остановится преждевременно, если на область значений параметров наложены несколько ограничений (отражающихся в штрафном значении; см. выше), которые пересекаются, приводя к обрыванию “гребня”.

36. Показатели корреляции и детерминации для нелинейных моделей регрессии