Определение тесноты связи и оценка существенности уравнения регрессии

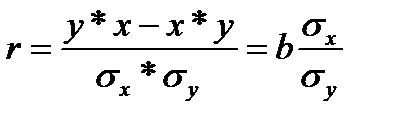(23.1)

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такового показателя выступает линейный коэффициент корреляции r_. Одна из формул линейного коэффициента корреляции имеет вид:

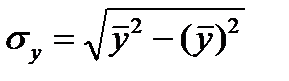(23.2) 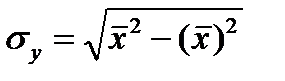(23.3) 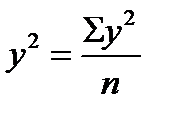(23.4)

Коэффициент корреляции находится в пределах: -1< r <1. Если b>0, то 0<r<1, и, наоборот, при b<0, -1< r<0.

Линейный коэффициент корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютного значения линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При нелинейном виде модели связь может оказаться достаточно тесной.

Квадрат линейного коэффициента корреляции называется коэффициентом детерминации. Он характеризует долю дисперсии результативного показателя y, объясняемую регрессией.

Соответственно величина 1-r² характеризует долю дисперсии у, вызванную влиянием остальных, неучтенных в модели, факторов.

После того как построено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных ее параметров.

Оценка значимости уравнения регрессии в целом производится с помощью F-критерия Фишера.

С F-критерием тесно связана характеристика, называемая числом степеней свободы, которая применительно к исследуемой проблеме показывает, сколько независимых отклонений из n-возможных

требуется для образования данной суммы квадратов.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммы квадратов.

Число степеней свободы для факторной суммы квадратов равно 1, для общей суммы квадратов равно (n-1), для остаточной суммы квадратов составляет (n-2).

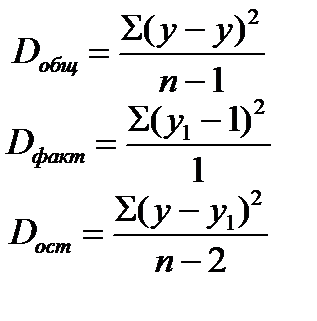(23.5)

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получаем дисперсию на одну степень свободы:

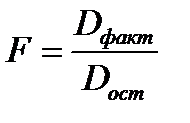(23.6)

Сопоставляя факторную и остаточную дисперсию на одну степень свободы, получим величину F- отношения (F - критерий):

Величина F- критерия связана с коэффициентом детерминации r² :

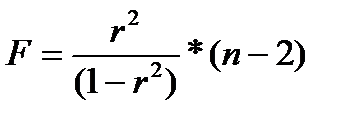(23.7)

F - критерий для проверки нулевой гипотезы H₀: D_факт = D_îñò.

Т.е. если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Это дает основание считать, что влияние объясняющей переменной х модели несущественно, а, следовательно, общее качество модели невысоко.

22. Частные коэффициенты корреляции для линейной модели регрессии с двумя переменными

Ранжирование факторов, участвующих в множественной линейной регрессии, можно достичь с помощью частных коэффициентов корреляции для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Так же, частные показатели корреляции широко используются при отборе факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Формула коэффициента частной корреляции имеет вид:

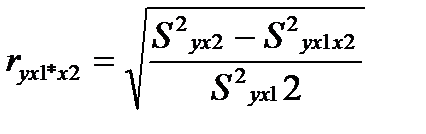(24.1)

Данные показатели частной корреляции называются коэффициентами или индексами частной корреляции первого порядка. Они показывают взаимосвязь между двумя переменными при стабилизации влияния одного из факторов.

Если до сих пор в качестве факторов мы рассматривали только экономические переменные, принимающие количественные значения, то возможно, может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Например, такие атрибутивные признаки как профессия, пол, образование климатические условия и т.д. имеют несколько качественных уровня. Чтобы ввести такие переменные в модель необходимо их преобразовать в количественные переменные. Переменные такой конструкции называются фиктивными.

Рассмотрим пример. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены.

В общем виде данное уравнение имеет вид: ,

где y - количество потребляемого кофе, x - цена.

Различия в потреблении кофе проявятся в различии средних `у<sub>1</sub> и`у₂. Вместе с тем сила влияния х на у может быть одинаковой, т.е. .

В этом случае можно ввести общее уравнение регрессии с включением в него фактора «пол» в виде фиктивной переменной:

где z₁, z₂ – фиктивные переменные.

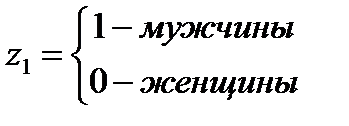
Рассмотренная модель с фиктивными переменными, выступающими как факторы, обладает наибольшими прогностическими возможностями. Однако на практике может возникнуть необходимость построения модели, в которой фиктивная переменная должна играть роль результата. Подобного рода модели применяются в социологии, при обработке данных социологических опросов. В качестве у - рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет», т.е. зависимая переменная у, имеет два значения 1 - («да») и 0 - («нет»).

23. Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными