Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор.

Понятие эконометрики

Эконометрика – это наука о применении статистических и математических методов в экономическом анализе для проверки правильности экономических теоретических моделей и способов решения экономических проблем.

Слово “эконометрика” – соединение 2-х слов – экономика (наука об экон. системах), метрика (наука об измерениях). Со временем, требовалось оценить точно возникающие связи между экономическими объектами (труд. ресурсами, ср. возраст рабочего, уровень безработицы, з/пл и т.д.) т.к. эти понятия носят как правило случайный характер, то без таких понятий как регрессия, корреляция, эконометрическая модель, временной ряд не обойтись. Обычно, те объекты, которые носят независимый характер, в экономике называют фактор признаками.

Эконометрика как наука расположена где–то между экономикой, статистикой и математикой, но ни одно из этих наук неспособна в отдельности, заменить эконометрику.

Эконометрические методы основаны на анализе связей между различными экономическими показателями (факторами) на основании статистических данных с использованием аппарата теории вероятностей и математической статистики. При помощи этих методов можно выявлять новые, ранее не известные связи, уточнять или отвергать гипотезы о существовании определенных связей между экономическими показателями, предлагаемые экономической теорией.

К основным задачам эконометрики можно отнести следующие:

- построение эконометрических моделей, то есть представление экономических моделей в математической форме. Данную проблему принято называть проблемой спецификации.

- оценка параметров построенной модели. Это этап параметризации.

- проверка качества найденных параметров модели и самой модели в целом. Иногда этот этап называют верификаций.

- использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания.

Эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классичес­ких статистических методов:

• асимметричности связей;

• мультиколлинеарности объясняющих переменных;

• закрытости механизма связи между переменными в изолиро­ванной регрессии;

• эффекта гетероскедастичности, т. е. отсутствия нормального распределения остатков для регрессионной функции;

• автокорреляции;

• ложной корреляции;

• наличия лагов.

Эконометрическое исследование включает решение следующих проблем:

• качественный анализ связей экономических переменных -выделение зависимых и независимых переменных;

• подбор данных;

• спецификация формы связи между у и х,

• оценка параметров модели;

• проверка ряда гипотез о свойствах распределения вероятнос­тей для случайной компоненты (гипотезы о средней, диспер­сии и ковариации);

• анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление перемен­ных, ответственных за мультиколлинеарность;

• введение фиктивных переменных;

• выявление автокорреляции лагов;

• выявление тренда, циклической и случайной компонент;

• проверка остатков на гетероскедастичность;

• проверка условия идентификации;

• проблемы идентификации и оценивания параметров.

2. Основные виды эконометрических моделей

Виды моделей подразделяются в зависимости от со­ответствующей теории связи между переменными. В урав­нении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией.

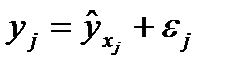
где y_j — фактическое значение результативного признака;

y_xj -теоретическое значение результативного признака.

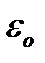— случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.

Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

От правильно выбранной спецификации модели за­висит величина случайных ошибок: они тем меньше, чем в боль­шей мере теоретические значения результативного признака 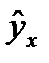подходят к фактическим данным у.

В парной регрессии выбор вида математической функции 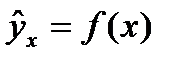может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.

Графи­ческий метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.

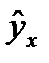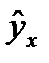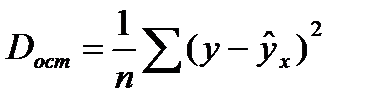Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии D_ост, рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у = , то D_ocm =0. Если имеют место отклонения фактических данных от теоретических (у — ) то . (2.2)

Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 — 7 раз превышать число рассчитывае­мых параметров при переменной х.

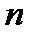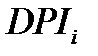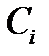Пусть, например, мы имеем данные о размерах располагаемого дохода ( disposable personal income) DPI и расходов на личное потребление (personal consumption) C для семейных хозяйств, так что и , соответственно, представляют располагаемый доход и расходы на личное потребление 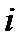-го семейного хозяйства.

Простейшей моделью связи между 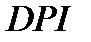и 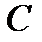является линейная модель связи. Если разместить на плоскости в прямоугольной системе координат точки 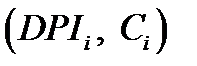с абсциссами 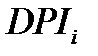и ординатами 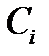(такое расположение точек называется диаграммой рассеяния - scatterplot), то, как правило, эти точки вовсе не будут лежать на одной прямой вида 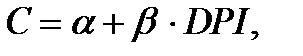соответствующей линейной модели связи. Вместо этого, они будут образовывать облако рассеяния, вытянутое в некотором направлении. В таком случае соотношение между 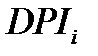и 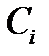принимает форму

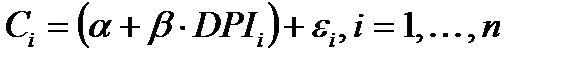(2.3)

(модель наблюдений), где слагаемое

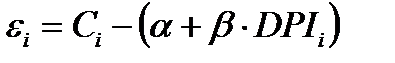(2.4)

представляет отклонение реально наблюдаемых расходов на потребление 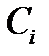от значения 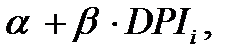предсказываемого гипотетической линейной моделью связи для 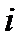-го семейного хозяйства. Эти отклонения отражают совокупное влияние на конкретные значения 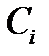множества дополнительных факторов, не учитываемых принятой моделью связи.

Предложив для описания имеющихся статистических данных модель, учитывающую указанные отклонения от теоретической модели линейной связи между 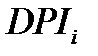и 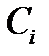(модель наблюдений), исследователи сталкиваются с вопросом о том, каковы значения 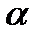и 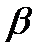в этой модели.

3. Эконометрическое моделирование

В эконометрических исследованных существенным является использование моделей. Процесс построения моделей называется эконометрическим моделированием. Модели должны быть “настолько простыми, насколько возможно, но не проще”, сказал Эйнштейн.

Рассмотрим пример.

Пусть необходимо проанализировать зависимость спроса Q на некоторый товар от цены P на этот товар. На основе экономической теории известно, что с ростом цены объем спроса сокращается. Опираясь на это утверждение можно предложить несколько математических зависимостей, отражающих этот факт. Например,

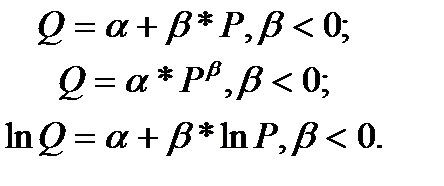
Необходимо отметить, что любая из моделей будет лишь упрощением реальности и всегда содержит определенную погрешность. Поэтому из всех предлагаемых моделей с помощью статистических методов отбирается та, которая в наибольшей степени соответствует реальным эмпирическим данным и характеру зависимости.

Далее идет этап параметризации, то есть оценка параметров (в нашем случае α и β ) так как эта оценка осуществляется на основе имеющихся статистических данных, то вопрос точности (качества ) статистической информации является одним из ключевых при построении модели.

Затем проверяется качество найденных оценок, а также соответствие модели эмпирическим данным и теоретическим предпосылкам (этап верификации). Данный анализ в основном осуществляется по схеме проверки статистических гипотез. На этом этапе совершенствуется не только форма модели, но и уточняется состав ее объясняющих переменных (возможно спрос на товар определяется не только его ценой, но и другими факторами, например, располагаемым доходом).

Если модель удовлетворяет требованиям качества, то она может быть использована для прогнозирования, либо для анализа внутреннего механизма исследуемых процессов.

Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности.

Математические модели позволяют более полно исследовать и понимать сущность происходящих процессов, анализировать их.

В эконометрических исследованиях используют разные типы моделей. Но можно выделить три основных класса моделей, которые применяются в эконометрике: модели временных рядов, регрессионные модели ( с одним уравнением) и системы одновременных уравнений.

Кроме этого используют также и другие типы кривых, например:

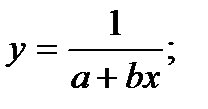
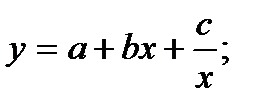
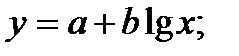
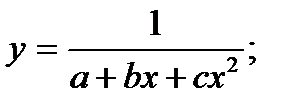
4. Классификация видов эконометрических переменных и типов данных

В эконометрических исследованиях используют два типа данных: пространственные данные (cross – sectional data) и временные ряды(time – seriesdata).

Пространственные данные – это данные, по какому- либо экономическому показателю, полученные для разных однотипных объектов (фирм, компаний, регионов).

Временные ряды – это данные, характеризующие один и тот же объект, но в различные моменты времени.

Примерами пространственных данных являются, например, площадь Саратовской области, количество промышленных предприятий на этой территории, средний уровень зарплаты по разным городам в определенный период времени.

Примерами временных рядов могут быть, например, ежегодные финансовые отчеты предприятия в налоговую инспекцию, ежемесячные отчеты о проделанной работе в деканате ВУЗа.

Например: х₁ – время обучения, х₂ – длительность и насыщенность занятий, х₃ – количество занятий – это все независимые переменные – экзогенные переменные (фактор признаки).

Аналогично, у₁ – уровень знаний выпускника, у₂ – цена обучения, у₃ – срок окупаемости затрат, у₄ – инвестиции в образование – зависимые переменные – эндогенные переменные (результативные признаки).

Не всегда затраты ведут к максимизации прибыли. Чтобы написать ту или иную зависимость применяют уравнение регрессии.

Уравнение регрессии – уравнение, связывающее между собой фактор признаки и результативные признаки. Уравнение регрессии бывают линейные и нелинейные. Сама регрессия бывает парная (зависимость между 1-им фактор признаком и результатом) и множественная.

y = y(x) (4.1) (значение между 1-им факторным признаком и результатом)

y = a + bx (4.2) (парная линейная регрессия, т.к. х и у участвуют в 1-ой степени, а и b – параметры регрессии имеющие экономический смысл).

Чтобы учесть возникающие помехи (погрешности в уравнении (4.2)) обычно пишут: у = a + bx + e, где e – искажение модели, учитывающее ряд других фактор признаков не явно участвующих в процессе.

Существуют и другого вида регрессии:

1) Линейные – по фактор признаку.

2) Нелинейные – по параметрам.

Например: (регрессия линейная, а и b под зн. log)

Однако, часть нелинейных регрессий легко сводится к лин. регрессиям:

Например: y = Ax + B, где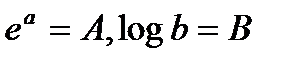

Однако, сущ. ур-ия регрессии не сводящиеся никаким способом к линейным.

Например: 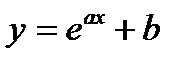(здесь регрессия нелинейная по фактор признаку х и по параметрам а и b)

Теория корреляции учитывает тесноту связи между признаками х и у.

Основными характеристиками служат:

линейный коэффициент парной корреляции;

средняя ошибка аппроксимации модели

5. Общая модель парной регрессии. Методы определения регрессионной модели

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными y и x, т.е. модель вида:

y = f(x), (5.1)

где у – зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная, (признак – фактор).

Строится простая (парная) регрессия в случае, когда среди факторов, влияющих на результативный показатель, есть явно доминирующий фактор.

В парной регрессии выбор вида математической функции y_х=f(x), может быть осуществлен графическим, аналитическим, экспериментальным методами.

Наиболее наглядным методом определения регрессионной модели является графический. Он основан на поле корреляции, которое строится в прямолинейной системе координат.

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии, который основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии y в зависимости от объема выпускаемой продукции x.

Общее потребление электроэнергии y можно подразделить на две части:

- не связанное с производством продукции а;

1. Часто встречаются факторы, которых следовало бы включить в регрессионное уравнение, но невозможно этого сделать в силу их количественной неизмеримости. Возможно, что существуют также и другие факторы, которые оказывают такое слабое влияние, что их в отдельности не целесообразно учитывать, а совокупное их влияние может быть уже существенным. Кроме того, могут быть факторы, которые являются существенными, но которые из-за отсутствия опыта таковыми не считаются. Совокупность всех этих составляющих и обозначено в (5.1) через ε.

2. Агрегирование переменных. Рассматриваемая зависимость (5.1) – это попытка объединить вместе некоторое число микроэкономических соотношений. Так как отдельные соотношения, имеют разные параметры, попытка объединить их является аппроксимацией. Наблюдаемое расхождение приписывается наличию случайного члена ε.

3. Выборочный характер исходных данных. Поскольку исследователи чаще всего имеет дело с выборочными данными при установлении связи между у и х, то возможны ошибки и в силу неоднородности данных в исходной статистической совокупности. Для получения хорошего результата обычно исключают из совокупности наблюдения с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Следует стремиться избегать возникновения этой проблемы, используя подходящую математическую формулу, но любая формула является лишь приближением истинной связи у и х и существующее расхождение вносит вклад в остаточный член.

6. Нормальная линейная модель парной регрессии

Линейная регрессия сводится к нахождению уравнения вида 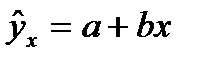или 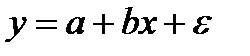. (6.1)

Уравнение вида 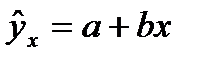позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.

Построение линейной регрессии сводится к оценке ее пара­метров а и в.

Оценки параметров линейной регрессии могут быть найдены разными методами.

1. 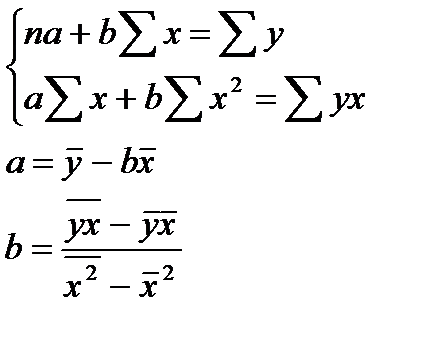(6.2)

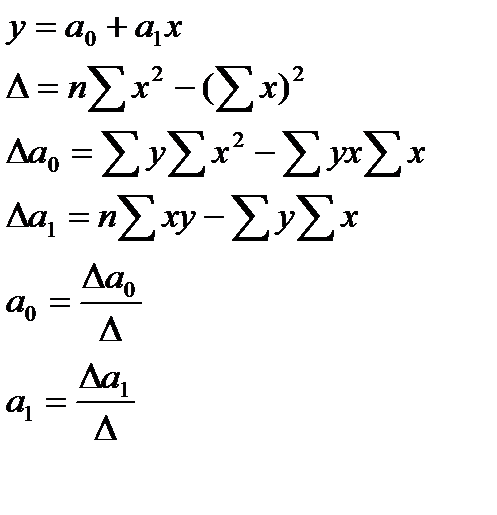2. (6.3)

Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.

Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_xy. Существуют разные модификации формулы линейного коэф­фициента корреляции.

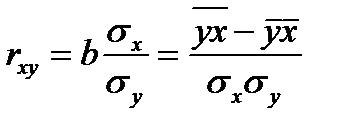(6.4)

Линейный коэффициент корреляции находится и границах: -1≤.r_xy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.r_xy ≤ 1 и наоборот при b<0 -1≤.r_xy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 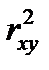, называемый коэффициентом детерминации. Коэффициент детермина­ции характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина 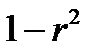характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

7. Оценивание неизвестных коэффициентов модели парной регрессии

Оценивание неизвестных коэффициентов модели парной регрессии. происходит следующими методами:

- метод наименьших квадратов (МНК);

- метод максимального правдоподобия.

Для оценки неизвестных коэффициентов модели парной регрессии составляют функцию правдоподобия, равную произведению плотностей вероятности отдельных наблюдений. при этом все σ _t будем считать независимыми:

(7.1)

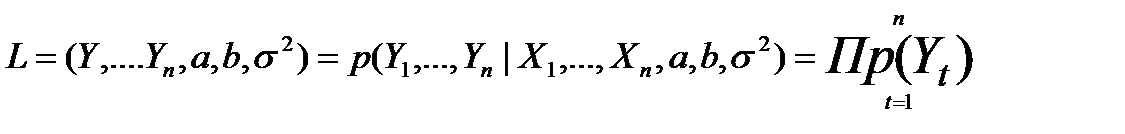
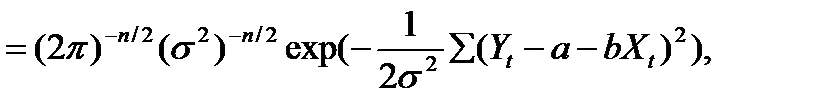(7.2)

где р обозначает плотность вероятности, зависящую от Х_t У_t, и параметров а, b,σ².

Отметим, что оценки неизвестных параметров а, b совпадают с оценками метода наименьших квадратов

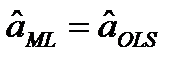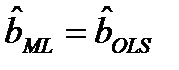, . Оценка максимального правдоподобия для σ² не совпадает с 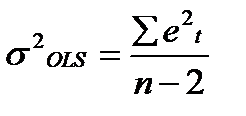которая, является несмещенной оценкой дисперсии ошибок. Таким образом, 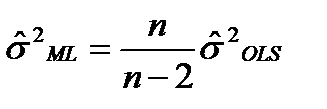(7.6) состоятельной оценкой σ².

На оценивание неизвестных коэффициентов существенное значение оказывает случайная величина, которая называется называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

Причин существования случайной составляющей несколько.

1. Не включение объясняющих переменных. Соотношение между y и x является упрощением. В действительности существуют и другие факторы, влияющие на y, которые не учтены в (2.1). Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой у = а+bх.

Часто встречаются факторы, которых следовало бы включить в регрессионное уравнение, но невозможно этого сделать в силу их количественной неизмеримости. Возможно, что существуют также и другие факторы, которые оказывают такое слабое влияние, что их в отдельности не целесообразно учитывать, а совокупное их влияние может быть уже существенным. Кроме того, могут быть факторы, которые являются существенными, но которые из-за отсутствия опыта таковыми не считаются. Совокупность всех этих составляющих и обозначено в (2.1) через ε.

2. Агрегирование переменных. Рассматриваемая зависимость (2.1) – это попытка объединить вместе некоторое число микроэкономических соотношений. Так как отдельные соотношения, имеют разные параметры, попытка объединить их является аппроксимацией. Наблюдаемое расхождение приписывается наличию случайного члена ε.

3. Выборочный характер исходных данных. Поскольку исследователи чаще всего имеет дело с выборочными данными при установлении связи между у и х, то возможны ошибки и в силу неоднородности данных в исходной статистической совокупности. Для получения хорошего результата обычно исключают из совокупности наблюдения с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Следует стремиться избегать возникновения этой проблемы, используя подходящую математическую формулу, но любая формула является лишь приближением истинной связи у и х и существующее расхождение вносит вклад в остаточный член.

8. Классический метод наименьших квадратов для модели парной регрессии

При наличии объективной тенденции поддержания линейной связи между переменным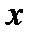и и 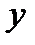естественно рассмотреть линейную модель наблюдений

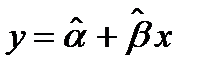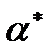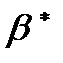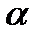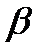, которую так же можно получить, исходя из принципа наименьших квадратов. Согласно этому принципу, среди всех возможных значений , , претендующих на роль оценок параметров и , следует выбирать такую пару 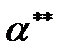, , 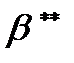для которой

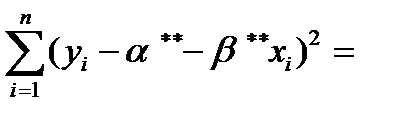
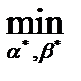
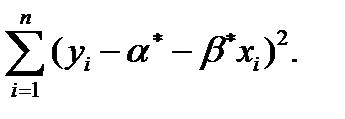(8.9)

Иначе говоря, выбирается такая пара 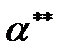, , 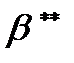для которой сумма квадратов невязок оказывается наименьшей. Получаемые при этом оценки называются оценками наименьших квадратов.

При построении оценок наименьших квадратов заранее не требуется, чтобы соответствующая прямая проходила через точку 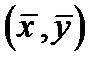; этот факт является свойством оценок наименьших квадратов. Определим, как практически найти указанные оценк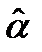и и .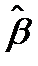

Если прямая 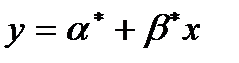проходит через точку 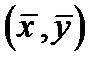, то тогда 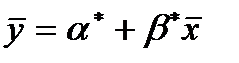, так что

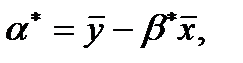(8.11)

и для поиска «наилучшей» прямой достаточно определить ее угловой коэффициент 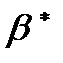. Изменяя значения 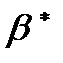и следя за изменением значений 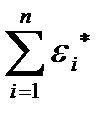, можем, найти искомое 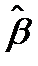с любой наперед заданной точностью.

Использование непосредственного перебора значений 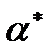, 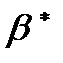с целью минимизации суммы квадратов

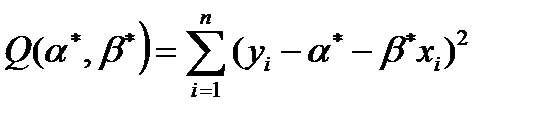(8.12)

при реализации метода наименьших квадратов также возможно, хотя и требует, конечно, существенно больших вычислительных усилий.

Получать оценки наименьших квадратов можно аналитически, сначала вычисляя параметры 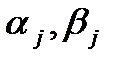отдельных прямых, а затем взвешивая полученные значения. Однако, существует еще один способ получения точных формул для 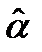и 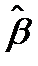, исходящий из принципа наименьших квадратов.

Согласно этому принципу, оценк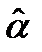и и 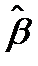находятся путем минимизации суммы квадратов

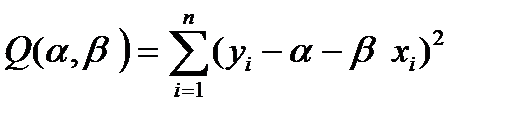(8.16)

по всем возможным значениям 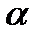и 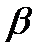при заданных (наблюдаемых) значениях 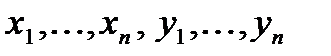. Функция 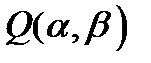как функция двух переменных описывает поверхность 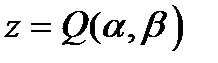в трехмерном пространстве с прямоугольной системой координат 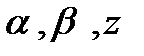, и дело сводится к известной математической задаче поиска точки минимума функции двух переменных.

Такая точка находится путем приравнивания нулю частных производных функции 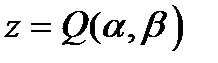по переменным 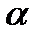и 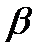, т. е. приравниванием нулю производной функции 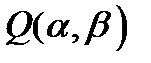как функции только от 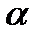при фиксированном ,

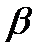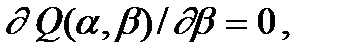(8.17)

и производной функции 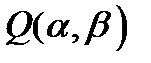как функции только от 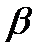при фиксированном ,

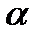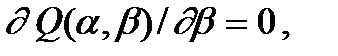
Это приводит к так называемой системе нормальных уравнений

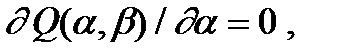
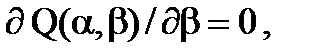
решением которой и является пара 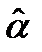, 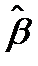. Остается заметить, что согласно правилам вычисления производных,

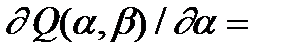
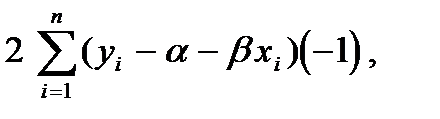(8.18)

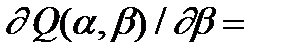
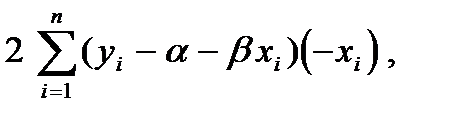(8.19)

так что искомые значения 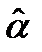, 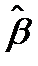удовлетворяют соотношениям

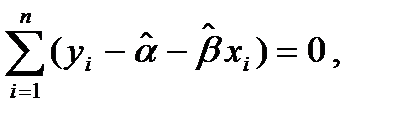
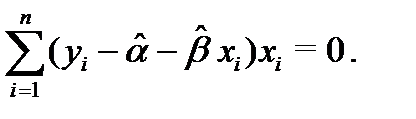(8.20)

9. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

В теории изучения эконометрики как предполагается, что имеется точная информация о рассматриваемой случайной переменной, в частности — об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распре деления (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из n наблюдений и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки. Способ оценивания — это общее правило, или формула, в то время как значение оценки — это конкретное число, которое меняется от выборки к выборке

В табл. 5 приведены формулы оценивания для двух важнейших характеристик генеральной совокупности. Выборочное среднее обычно дает оценку для математического ожидания, а формула 2 в табл. 5 — оценку дисперсии генеральной совокупности.

Таблица 5

Характеристики генеральной совокупности	Формулы оценивания
Среднее, μ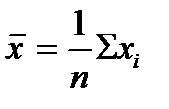
Дисперсия, σ2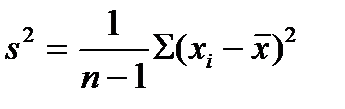

Отметим, что это обычные формулы оценки математического ожидания и дисперсии генеральной совокупности, однако не единственные. Возможно, вы настолько привыкли использовать х в качестве оценки для μ, что даже не задумывались об альтернативах. Конечно, не все формулы оценки, которые можно представить, одинаково хороши. Причина, по которой в действительности используется х , в том, что эта оценка в наилучшей степени соответствует двум очень важным критериям — не смещенности и эффективности. Эти критерии будут рассмотрены ниже.

Оценки как случайные величины

Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х — случайная переменная и, следовательно, случайной величиной является и функция набора ее значений. Возьмем, например, — оценку математического ожидания:

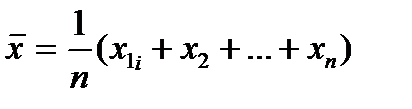(9.1)

Мы только что показали, что величина х в i-м наблюдении может быть разложена на две составляющие: постоянную часть ц и чисто случайную составляющую u_i,:

х_i = μ + u_i (9.2)

Следовательно,

х = μ + u (9.3)

где u - выборочное среднее величин u_i,.

0тсюда можно видеть, что х , подобно х, имеет как фиксированную, так и чисто случайную составляющие. Ее фиксированная составляющая - μ, то есть математическое ожидание х, а ее случайная составляющая - u , то есть среднее значение чисто случайной составляющей в выборке.

Величина х считается нормально распределенной. Можно видеть, что распределения, как х, так и х , симметричны относительно μ - теоретического среднего. Разница между ними в том, что распределение х уже и выше. Величина х, вероятно, должна быть ближе к μ, чем значение единичного наблюдения х, поскольку ее случайная составляющая u есть среднее от чисто случайных составляющих u₁, u₂,… u_n, и в выборке, которые, по-видимому, «гасят» друг друга при расчете среднего. Далее, теоретическая дисперсия величины и составляет лишь часть теоретической дисперсии u.

10. Пример оценки коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии

Пример. Доходы семы. Пусть Inc обозначает реальный доход семьи, Expend - ее реальные расходы. Для того чтобы исследовать зависимость расходов от доходов, оценим коэффициенты регрессии Expend на Inc и константу.

Для всех типов семей (количество наблюдений 3594)

Expend = 4663.3 + 0.686 Inc R² = 0.21, s = 11307. (10.1)

(233.6) (0.0223)

В скобках приведены стандартные ошибки коэффициентов регрессии. Соответствующие t- статистики равны 19.96 и 30.81, т. е. коэффициенты статистически достоверно отличаются от нуля. Однако значение коэффициента детерминации R² невелико. Это объясняется, конечно, разнородностью семей как по составу, так и по другим факторам, таким, как место проживания, структура расходов, состав семьи и т. п. Таким образом, для более однородной выборки семей мы вправе ожидать увеличения значения коэффициента детерминации.

Lля семей, состоящих из одного человека (количество наблюдений 509):

Ехреnd = 3229.2 + 0.355 Inc , R² = 0.39, s = 4567. (10.2)

(182.0) (0.0162)

Как и раньше, коэффициенты являются значимыми — t-статистики равны соответственно 17.74 и 20.70. Как мы и ожидали, качество подгонки улучшилось —коэффициент R² возрос с 0.21 до 0.39, а оценка стандартного отклонения остатков s уменьшилась с 11307 до 4567. Так как в семьях из одного человека нет расходов на содержание неработающих членов семьи (дети, престарелые), то на потребление тратится меньшая часть прироста дохода. Склонность к потреблению, определяемая как дЕхреnd/дInc, для семьи из одного человека равна 0.355, в то время как в среднем по всей выборке 0.686.

Обозначим через Nf количество членов в семье. Оценим ре грессию среднего расхода на члена семьи на средний доход члена семьи (количество наблюдений 3594):

Ехреnd/ Nf = 2387.2 + 0.447 Inc/ Nf , R² = 0.24, s = 4202. (10.3)

(76.8) (0.0133)

Значение R² увеличилось по сравнению с первой регрессией. Пере ход к удельным данным приводит к уменьшению дисперсии ошибок модели.

11. Оценка дисперсии случайной ошибки модели регрессии

В регрессионном уравнении всегда имеется сопутствующий параметр –дисперсия случайной ошибки σ².

Обозначим через 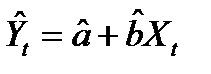прогноз значения Y_t в точке Х_t. Остатки регрессии е_t определяются из уравнения 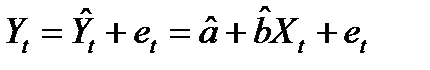(11.1)

Остатки е_t, так же как и ошибки ε_t, являются случайными величинами, но остатки наблюдаемы, а ошибки –нет.

В реальных исследованиях дисперсия ошибок σ² неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии а,b. При этом вместо дисперсий оценок получаем оценки дисперсий. При этом вместо σ² используется s².

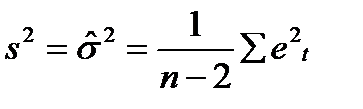11.2)

это несмещенная оценка дисперсии ошибок σ².

Также используется следующая формула для определения оценки дисперсии случайной ошибки.

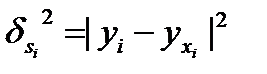- дисперсия ошибки при конкретном i-м значении фактора,

k_i- коэффициент пропорциональности, меняющийся с изменением величины фактора.

12. Состоятельность и несмещенность МНК-оценок

МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) 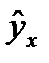ми­нимальна:

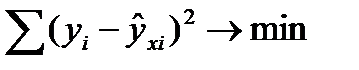(12.1)

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минималь­ной. 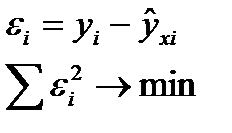(12.2)

Решается система нормальных уравнений

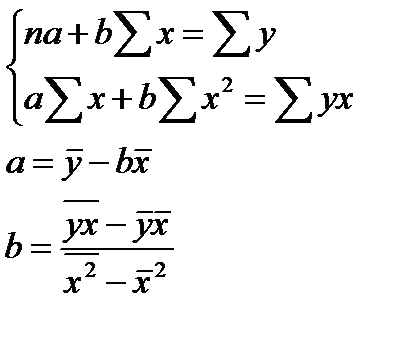(12.3)

Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяет­ся, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в парабо­ле второй степени y=a₀+a₁x+a₂x²+ε заменяя переменные x=x₁,x²=x₂, получим двухфакторное урав­нение линейной регрессии: у=а₀+а₁х₁+а₂х₂+ ε

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется харак­тер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное), значение результативного признака: приравнива­ем к нулю первую производную параболы второй степени: 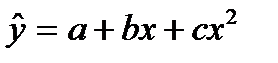, т.е. b+2cx=0 и x=-b/2c (12.4)

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

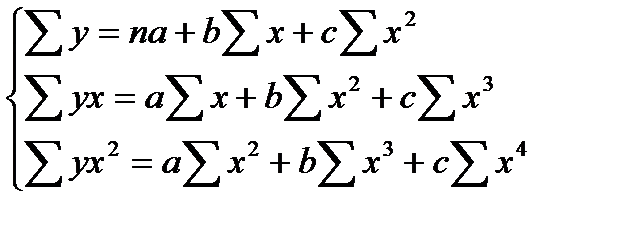(12.5)

Решение ее возможно методом определителей:

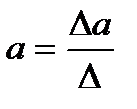(12.6)

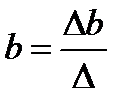(12.7)

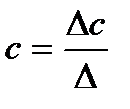(12.8)

При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей 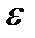, которая представляет собой ненаблюдаемую величину.

Исследования остатков 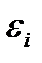- предполагают проверку наличия сле­дующих пяти предпосылок МНК:

1.случайный характер остатков;

2.нулевая средняя величина остатков, не зависящая от х_i;

3.гомоскедастичность—дисперсия каждого отклонения 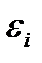,одинакова для всех значений х;

4.отсутствие автокорреляции остатков. Значения остатков 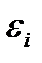, распределены независимо друг от друга;

5.остатки подчиняются нормальному распределению.

Рассмотрим предпосылки МНК

1) Проверяется случайный характер остатков 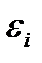, с этой целью строится график зависимости остатков 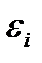от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки 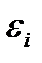, представляют собой случайные величины и МНК оправдан, те­оретические значения у_х хорошо аппроксимируют фактические значения y. В других случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию и за­ново строить уравнение регрессии до тех пор, пока остатки 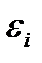, не будут случайными величинами.

2) Вторая предпосылка МНК относительно нулевой средней ве­личины остатков означает, что 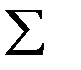(у — у_х) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю­чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков 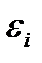от теоретических значений ре­зультативного признака у_х строится график зависимости случай­ных остатков 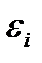от факторов, включенных в регрессию х_{i .} Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений x_j. Если же график показывает наличие зависимости 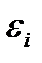и х_j то модель неадек­ватна. Причины неадекватности могут быть разные.

3) В соответствии с третьей предпосылкой МНК требуется, что­бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_j остатки 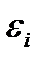, имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. Гомоскедастичность остатков означает, что дисперсия остат­ков 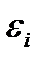- одинакова для каждого значения х.

4)Отсутствие автокор­реляции остатков, т. е. значения остатков 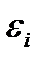распределены неза­висимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии.

13. Эффективность оценок МНК. Теорема Гаусса-Маркова

Имея набор наблюдений (Х_t, Y_t), t=1,…n, и модель 1-3ab, зададимся целью оценить все 3 параметра модели: a, b,σ².

Для наилучшей оценки параметров а и b применим теорему Гаусса- Маркова в предположениях модели 1-3ab:

1. Y_t = a + bX _t + ε _t, t = 1,…n;

2. Х_t - детерминированная величина;

3а. Еε _t = 0, Е (ε _t²) = V (ε _t) = σ²

3б. Е(ε _tε_s) =0 , при t ≠ s

Оценки 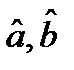, полученные по методу наименьших квадратов (МНК), имеют наименьшую дисперсию в классе всех линейных оценок.

Доказательство.

1. Проверим, что МНК –оценки 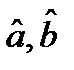являются несмещенными оценками истинных значений а,b. Следовательно:

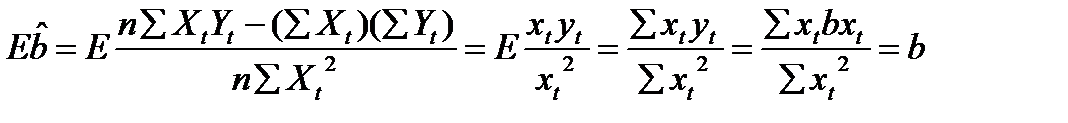(13.1)

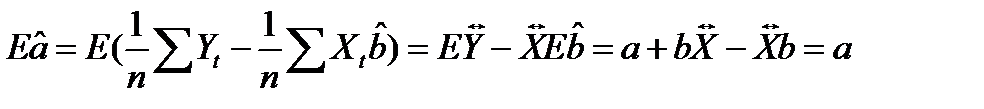(13.2)

вычислим дисперсии оценок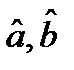

Представим 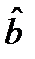в ви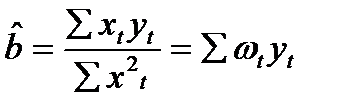де:

, где 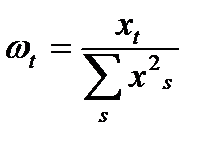(13.3)

Легко проверить, что w_t удовлетворяет следующим условиям:

1) 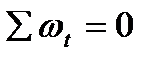(13.4)

2) 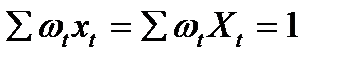(13.5)

3) 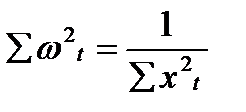(13.6)

4) 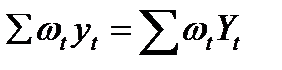(13.7)

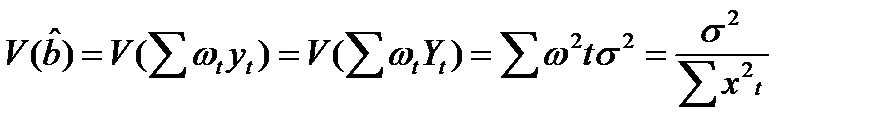(13.8)

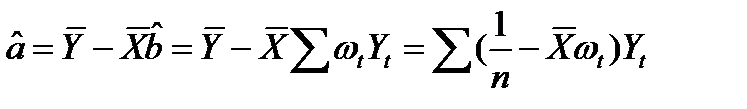(13.9)

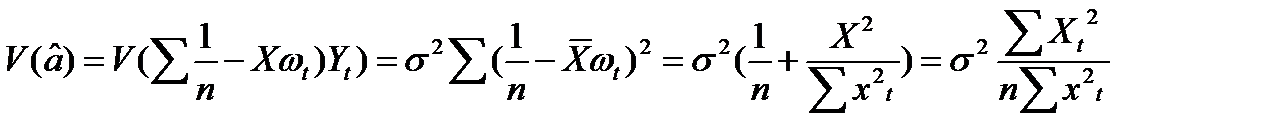(13.10)

Формула (13.10) получается с использованием тождества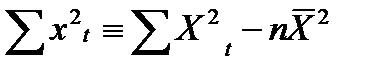

в качестве выводов произведем доказательство что МНК - оценка имеет наименьшую дисперсию среди всех несмещенных оценок.

Пусть 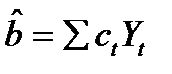-любая другая несмещенная оценка. Представим с_t в виде с_t =ω_t + d_t, тогда 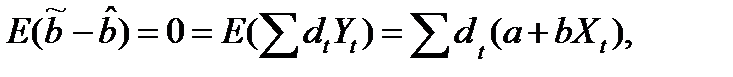(13.11)

для всех а,b. Отсюда

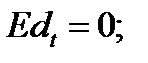
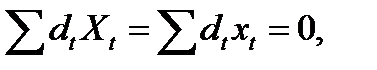(13.12)

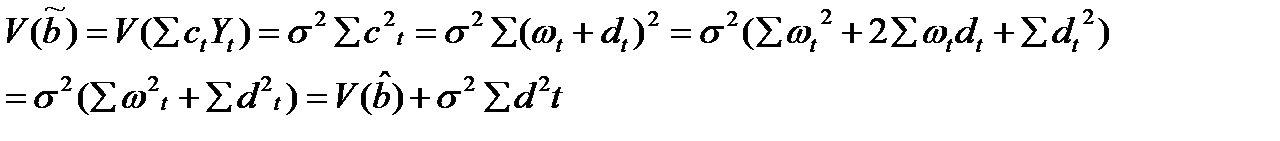Другими словами 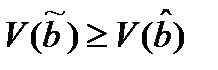, а это и есть доказательство теоремы Гаусса –Маркова.

14. Проверка гипотезы о значимости коэффициентов модели парной регрессии с помощью t – статистики Стьюдента.

Оценка статистической значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н₀ о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t – критерия Стьюдента.

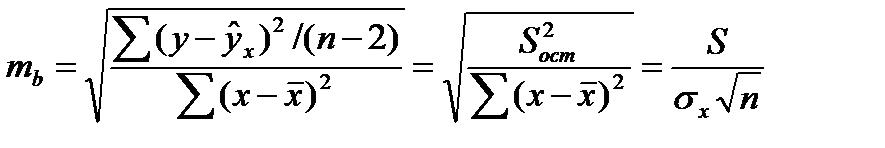(15.1)

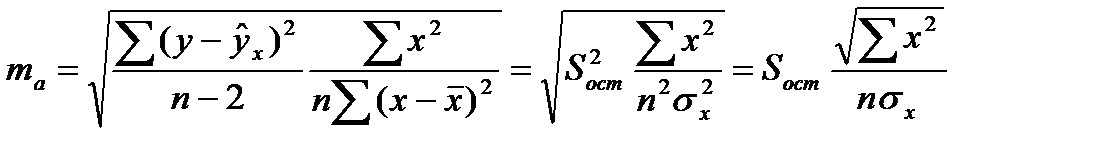(15.2)

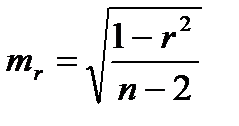(15.3)

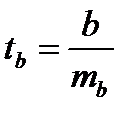(15.4) 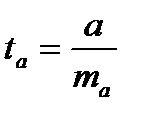(15.5) 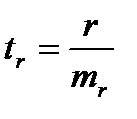(15.6)

Определяется стат. значимость параметров.

t_a ›T_табл - a стат. значим

t_b ›T_табл - b стат. значим

Находятся границы доверительных интервалов.

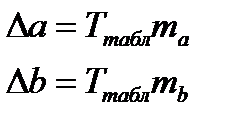(15.7) 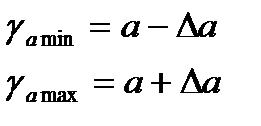(15.8) 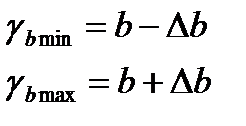(15.9)

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не явл.. стат. незначимыми и существенно отличается от 0.

15. Проверка гипотезы о значимости парного коэффициента корреляции

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера. При этом выдвигается нулевая ги­потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе­ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:

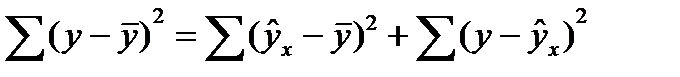(16.1)

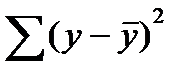- общая сумма квадратов отклонений

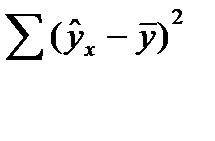- сумма квадратов отклонения объясненная регрессией 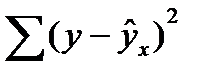- остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степе­ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для образования данной суммы квадратов.

Дисперсия на одну степень свободы D.

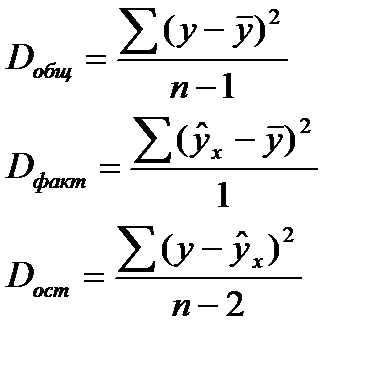(16.2)

F-отношения (F-критерий): 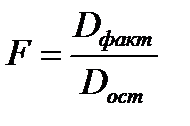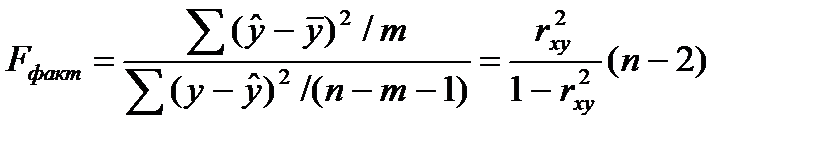(16.3)

Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз­работаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт > F_табл Н₀ отклоняется.

Если же величина окажется меньше табличной F_факт ‹, F_табл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Н_о не отклоняется.

Стандартная ошибка коэффициента регрессии

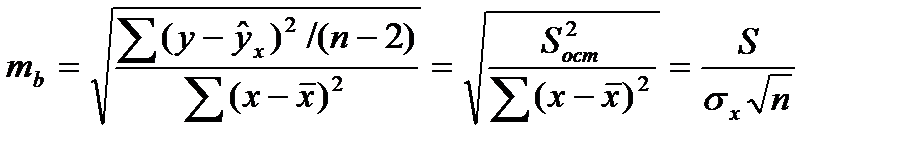(16.4)

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: 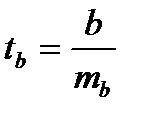которое

затем сравнивается с табличным значением при определенном уровне значимости 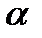и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

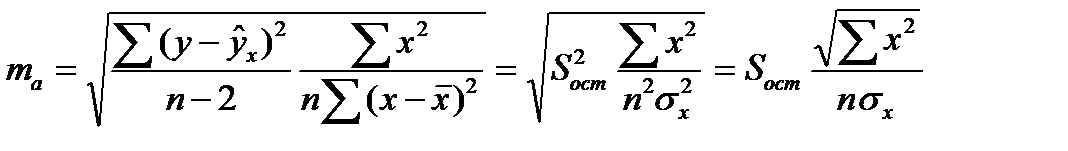(16.5) 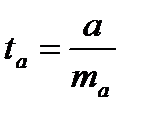(16.6)

Значимость линейного коэффициента корреляции проверя­ется на основе величины ошибки коэффициента корреляции т_r:

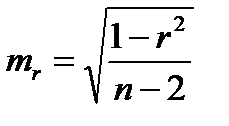(16.7) 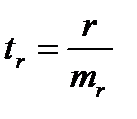(16.7)

Общая дисперсия признака х: 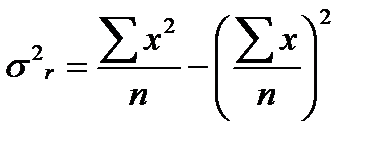(16.8)

Коэф. регрессии 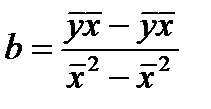(16.9)

Его величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации: 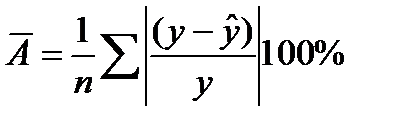(16.10)

16. Проверка гипотезы о значимости уравнения парной регрессии

Пусть выполняется условие, нормальной линейной регрессионной модели 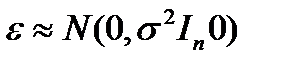,т.е. ε- многомерная нормально распределенная случайная величина, или что то же самое, Y_t имеют совместное нормальное распределение. тогда МНК –оценки коэффициентов регрессии 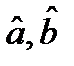имеют совместное нормальное распределение, так как они являются линейными функциями от Y_t.:

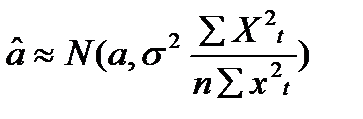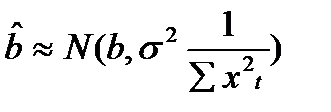, . (17.1)

Если гипотеза значимости уравнений парной регрессии не выполняется, то (17.1) является неверным, однако при условиях стабильности Х_t при росте n оценки a^, b^ имеют асимптотически нормальное распределение, т.е. (17.1) выполняется асимптотически при n → ∞.

Произведем проверку гипотезы о том, что b=b₀

Из (17.1) получаем 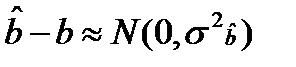, где 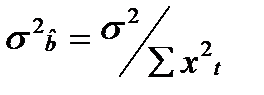. Оценка дисперсии оценки 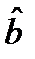получается из формулы 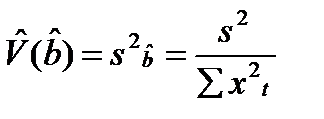. Таким образом,

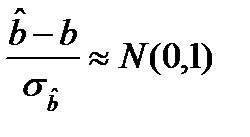, (17.2)

Следовательно

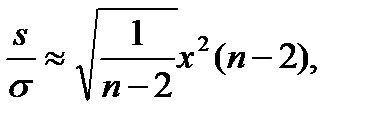(17.3)

т.е. по определению статистики Стьюдента, имеется

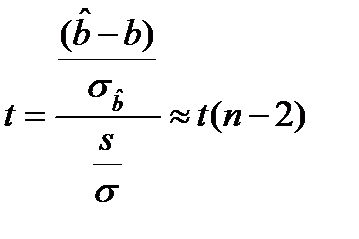(17.4)

и, так как

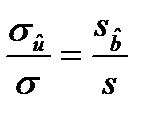, получаем 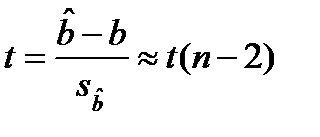(17.5)

Формулу (17.5) применяют для проверки гипотезы Н₀:b = b₀ против альтернативной гипотезы Н₁: b ≠ b₀. Предположим гипотезу Н₀ –верной на 95% уровне. с (n -2) степенями свободы:

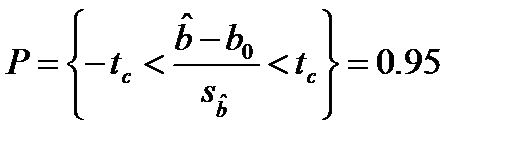(17.6)

Отвергая Н₀, принимаем верной Н₁ на 5% уровне значимости.

17. Пример проверки гипотезы о значимости регрессионных коэффициентов и модели парной регрессии в целом.

Рассмотрим значение коэффициента регрессии.

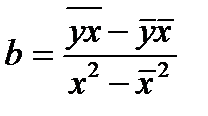(18.1)

Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Оценку коэффициента регрессии можно получить не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата 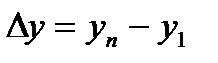сопоставляют с изменением фактора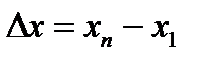

Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения 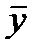вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы.

Если фактор не оказывает влияния на результат, то линия регрес­сии на графике параллельна оси ох и 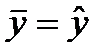.Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный вли­янием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригод­ность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариа­цию

Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у

Любая сумма квадратов отклонений связана с числом степе­ней свободы , т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n ис числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых откло­нений из п возможных требуется для образования данной суммы квадратов.

18. Линейная модель множественной регрессии

Регрессия может дать хороший результат при модели­ровании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономи­ческих переменных контролировать нельзя, т. е. не удается обес­печить равенство всех прочих условий для оценки влияния одно­го исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. пост­роить уравнение множественной регрессии:

y=a+b₁x₁+b₂+…+b_px_p+e; (20.1)

Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты bj — частные производные потребления у по соответствующим факторам

x_i: 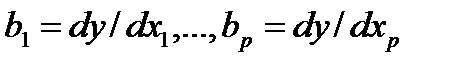, (20.2)

в предположении, что все остальные х_i постоянны. В 30-е гг. XX в. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неод­нократно обращались к проблеме ее совершенствования. Совре­менная потребительская функция чаще всего рассматривается как модель вида:

C=j(y,P,M,Z), (20.3)

где С — потребление; у — доход; Р — цена, индекс стоимости жизни; М — наличные деньги; Z — ликвидные активы.

При этом 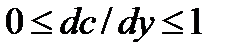.. (20.4)

Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает в себя два