Частные уравнения множественной регрессии. Индексы множественной и частной корреляции и их расчет

На основе линейного уравнения множественной регрессии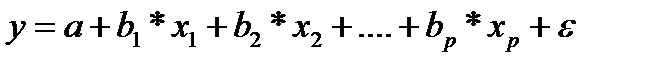

могут быть найдены частные уравнения регрессии:

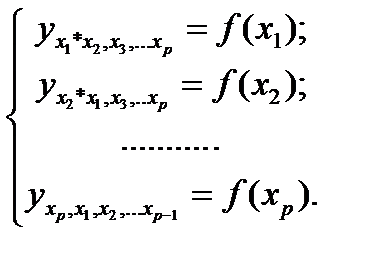(25.1)

т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х_i при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. В случае линейной регрессии частные уравнения имеют следующий вид:

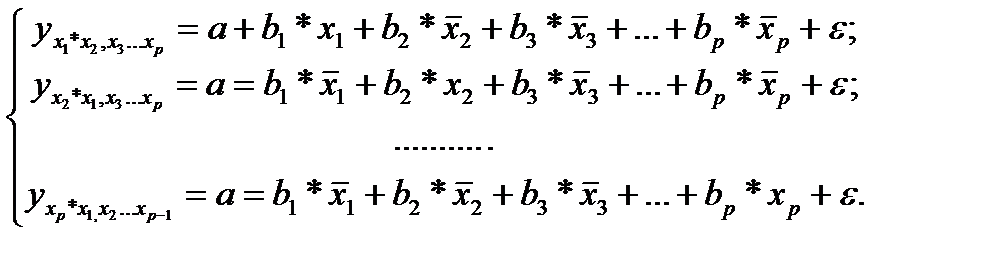(25.2)

Подставляя в эти уравнения средние значения соответствующих факторов получаем систему уравнений линейной регрессии, т.е. имеем:

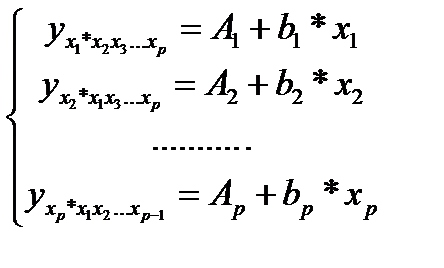(25.3)

где 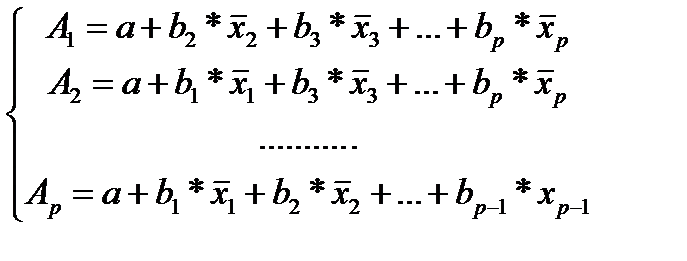(25.4)

Частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на низменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии (А_i).Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности

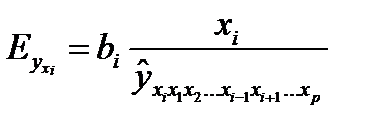(25.5)

На основании данной информации могут быть найдены средние по совокупности показатели эластичности: .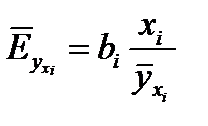

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту совместного влияния факторов на результат.

Независимо от вида уравнения индекс множественной корреляции рассчитывается по формуле:

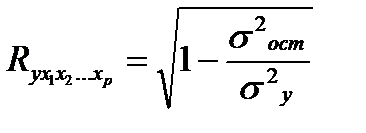, (25.6)

где σ²_y - общая дисперсия результативного признака,

σ²_ост - остаточная дисперсия .

Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Сравнивая индексы множественной регрессии и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. В частности, если дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции практически совпадает с индексом парной корреляции.

Если оценивается значимость влияния фактора х_i в уравнении регрессии, то определяется частный F- критерий:

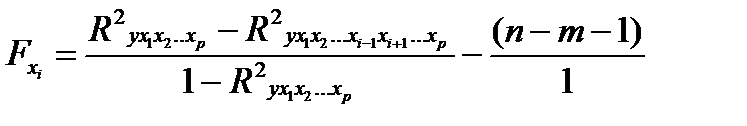(25.7)

Значимость коэффициентов чистой регрессии производится по t - критерию Стьюдента.

24. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Чем больше доля полученной разности в остаточной вариации, тем теснее связь между у и x₂ , при неизменности действия фактора x₁

Величина, рассчитываемая формулой:

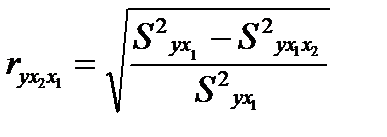(26.1)

называется индексом частной корреляции для фактора х₂:

Аналогично определяется индекс частной корреляции для фактора x_1.

Выражая остаточную дисперсию через показатель детерминации

S²_ост = σ²_у (1-r²), имеем формулу частной корреляции:

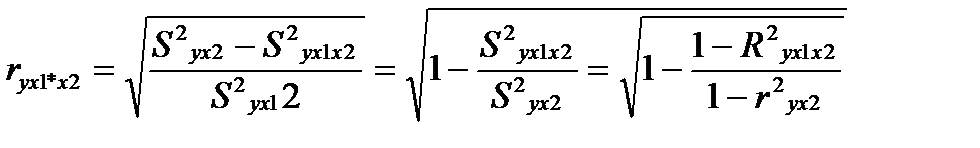(26.2)

25. Коэффициент множественной корреляции

Практическая значимость уравнения множественной регрессии оценивается показателем множественной корреляции

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым при знаком, или оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции можёт быть найден как индекс множественной корреляции:

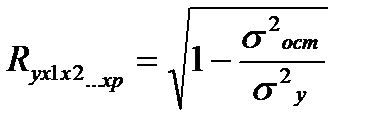(27.1)

, где

σ²_ост – остаточная дисперсия для уравнения у=f(x₁,x₂,… x_р)

σ²_у – общая дисперсия результативного признака

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Его пределы от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем I бором исследуемых факторов. Величина индекса множественно корреляции должна быть больше или равна максимальному парному индексу корреляции: -

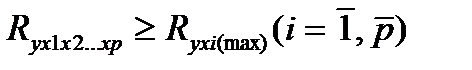(27.2)

Обоснованность включения факторов в регрессионный анализ приведет к существенному отличию показателя от индекса корреляции парной зависимости. При включении модель маловажных факторов происходит уравнение индекса множественной корреляции с индексом парной корреляции. Сравнивая индексы множественной и парной корреляции делают заключение о возможности включения в уравнение регрессии того или иного фактора.

Расчет индекса множественной Корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

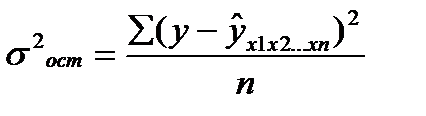(27.3)

Возможна и такая интерпретация формулы индекса множественной корреляции

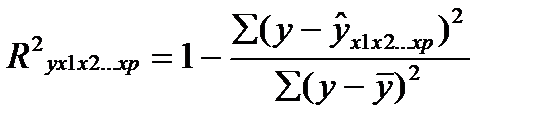(27.4)

26. Коэффициент множественной детерминации

Коэффициент детерминации –это квадрат показателем множественной корреляции.

Множественный коэффициент детерминации можно рассматривать как меру качества уравнения регрессии, характеристику прогностической силы анализируемой регрессионной модели: чем ближе R² к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными. Недостаток R² состоит в том, что его значение не убывает с ростом числа объясняющих переменных. В эконометрическом анализе чаще применяют скорректированный коэффициент детерминации R^²определяемый по формуле

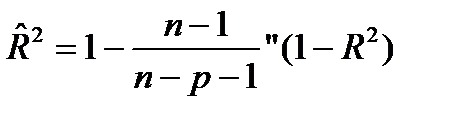(28.1)

который может уменьшаться при введении в регрессионную модель переменных, не оказывающих существенного влияния на зависимую переменную.

Если известен коэффициент детерминации R² то критерий значимости уравнения регрессии может быть записан в виде:

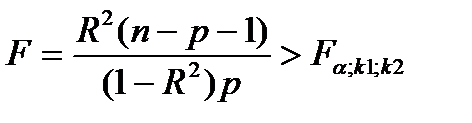(28.2)

где ‚ к1= р, к2 = n - р - 1, ибо в уравнении множественной регрессии вместе со свободным членом оценивается m = р + 1 параметров.

27. Проверка гипотезы о значимости частного и множественного коэффициентов корреляции

Проверка гипотез используется, когда необходим обоснованный вывод о значимости частного и множественного коэффициентов корреляции. При этом гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Множественный коэффициент корреляции заключен в пре делах 0 до1. Он не меньше, чем абсолютная величина любого парного или частного коэффициента корреляции с таким же первичным индексом.

С помощью множественного коэффициента корреляции (по мере приближения к 1 делается вывод о тесноте взаимосвязи, но не о ее направлении.

Частный коэффициент корреляции. Если переменные коррелируют друг с другом, то на величине парного коэффициента корреляции частично сказывается влияние других переменных. В связи с этим часто возникает необходимость исследовать частную корреляцию между переменными при устранении влияния одной/нескольких переменных

28. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

Основной предпосылкой регрессионного анализа является то, что только результативный признак (У) подчиняется нормальному закону распределения, а факторные признаки х 1 . Х 2 ..., х n могут иметь произвольный закон распределения. В анализе динамических рядов в качестве факторного признака выступает время t При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей между результативным (У) и факторными х 1 . Х 2 ..., х n признаками. В тех случаях, когда из природы процессов в модели или из данных наблюдений над ней следует вывод о нормальном законе распределения двух СВ - Y и X , из которых одна является независимой, т. е. Y является функцией X , то возникает соблазн определить такую зависимость “формульно”, аналитически.Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражаемая функцией Y=f( х 1 . Х 2 ..., х n ) является достаточно адекватным реальному моделируемому явлению или процессу в случае соблюдения следующих требований их построения. 1) Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями. 2) Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей. 3) Все факторные признаки должны иметь количественное (цифровое) выражение. 4) Наличие достаточно большого объема исследуемой выборочной совокупности. 5) Причинно-следственные связи между явлениями и процессами следует описывать линейной или приводимой к линейной формой зависимости. 6) Отсутствие количественных ограничений на параметры модели связи. 7) Постоянство территориальной и временной структуры изучаемойсовокупности. Соблюдение данных требований позволяет исследователю построить статистическую модель связи, наилучшим образом аппроксимирующую моделируемые социально-экономические явления и процессы. В случае успеха нам будет намного проще вести моделирование. Конечно, наиболее заманчивой является перспектива линейной зависимости типа Y = a + b · X . Подобная задача носит название задачи регрессионного анализа и предполагает следующий способ решения. Выдвигается следующая гипотеза H 0 : случайная величина Y при фиксированном значении величины X распределена нормально с математическим ожиданием М y = a + b · X и дисперсией D y , не зависящей от X . При наличии результатов наблюдений над парами X i и Y i предварительно вычисляются средние значения M y и M x , а затем производится оценка коэффициента b в виде b = = R xy что следует из определениякоэффициента корреляции. После этого вычисляется оценка для a в виде {2 - 16} и производится проверка значимости полученных результатов. Таким образом, регрессионный анализ является мощным, хотя и далеко не всегда допустимым расширением корреляционного анализа, решая всё ту же задачу оценки связей в сложной системе.

29. Определение мультиколлинеарности. Последствия мулыиколлицеарности. Методы обнаружения мультиколлинеарности

Мультиколлинеарность -это процесс, при котором между факторами происходит совокупное воздействие друг на друга

Наличие мультиколлинеарности факторов может означать, что некоторые факторы действуют синхронно. В итоге вариация в исходных данных зависима и невозможно оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Если рассматривается регрессия у = а + b * х + с * z + d * v + ε то для расчета параметров с применением МНК предполагается равенство:

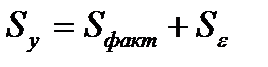(31.1)

где 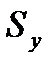— общая сумма квадратов отклонений Σ(у_i-у¯)²

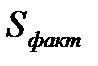— факторная сумма квадратов отклонений: Σ(у^_i-у¯)²

— остаточная сумма квадратов отклонений Σ(у^_i-у)²

Если же факторы интеркоррелированы, то данное равенство нарушается.

Включение в модель мультиколлинеарных факторов нежелательно по причинам:

• затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в чистом виде, т.к. факторы коррелированны. При этом параметры линейной регрессии утрачивают экономический смысл;

• оценки параметров ненадежны, появляются стандартные ошибки, которые меняются с изменением объема наблюдений (по величине и знаку), Модель нельзя анализировать и строить на ее основе прогнозы.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных Коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между ними была бы единичной, т.к. все элементы не находящиеся на диагоналях равны 0. Для уравнения включающее три объясняющих переменных,

у = а + b₁ * х₁ + b₂ * х₂ + b₃ * х₃ +ε, при этом матрица коэффициентов корреляции между факторами имела определитель равный единице.

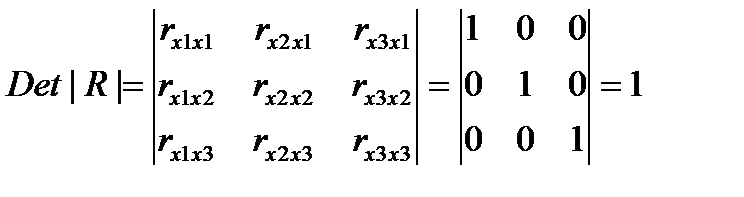(31.2)

Если же между факторами существует полная линейная зависимость и все Коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю.

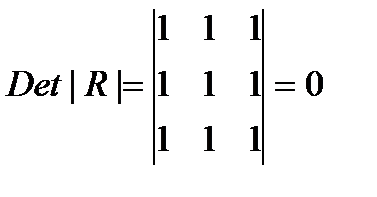(31.3)

Чем ближе к - нулю определитель матрицы межфакторной корреляции тем сильнее мультиколлинеарность факторов и ненадежнее результаты множествснной регрессии. Наоборот чем ближе к единице определитель матрицы межфакторной корреляции тем меньше мультиколлинеарность факторов.

30. Методы устранения мультиколлинеарности

Устраняя мультиколлинеарность факторов чаще всего используют приведенную форму. Для этого в уравнение регрессии подставляют рассматриваемый фактор, выраженный из другого уравнения.

В двухфакторной регрессии вида

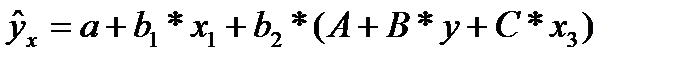(32.1)

сделав предобразования получим:

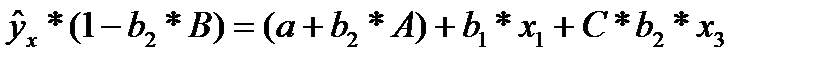(32.2)

Если исключить один из факторов, то мы придем к уравнению парной регрессии. Вместе с тем, можно оставить факторы в модели, но исследовать данное двух факторное уравнение регрессии совместно с другим уравнением, в котором фактор рассматривается как зависимая переменная. При (1-b₂*В) ≠ 0, делим первую и вторую части уравнения на (1-b₂*В), получаем:

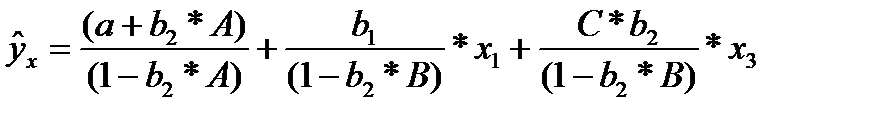(32.3)

Получили приведенную форму уравнения для определения результативного признака у. Это уравнение может быть представлено в виде (32.4)

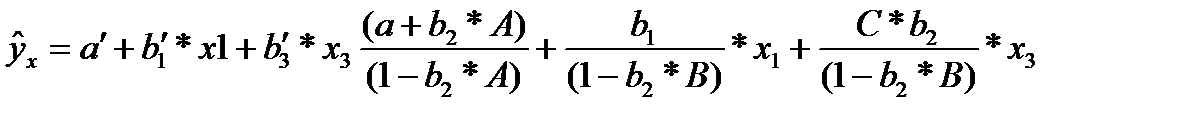
К нему для оценки параметров может быть применен метод наименьших квадратов.

Отбор факторов, включаемых в регрессию -основной этап практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут различны. Они приводят построение уравнение множественной регрессии соответственно к разным методикам.

Наиболее распространены методы построения уравнения множественной регрессии:

• метод исключения;

• метод включения;

• шаговый регрессионный анализ.

Каждый метод помогает устранить мультиколлинеарность позволяя производить отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

На первый Взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут полностью решать вопрос целесообразности включения в модель того определенного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. Отсев факторов можно проводить и по t-критерию Стьюдента для коэффициентов регрессии: из уравнения исключаются факторы с величиной t-критерия меньше табличного.

В заключении следует уточнить: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что пара метры уравнения регрессии оказываются статистически незначимыми, а Р-критерий меньше табличного значения.

31. Модели регрессии, нелинейные по факторным переменным

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы 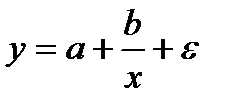, параболы второй степени 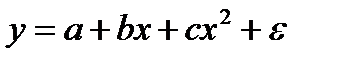и д.р.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

• регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

• полиномы разных степеней

• равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

• степенная

• показательная

• экспоненциальная

<1 2 345 6 7 >

Дата добавления: 2015-05-21; просмотров: 4163;