Адаптивные модели прогнозирования

Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивной модели является математическая модель, аргументом которой выступает – время.

При оценке параметров адаптивных моделей, в отличии от «кривых роста», наблюдениям (уровням ряда) присваиваются различные веса, в зависимости от того, насколько сильным признается их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность.

В качестве примера рассмотрим модель экспоненциального сглаживания Брауна. Модель Брауна может отображать развитие не только в виде линейной тенденции, или в виде случайного процесса, не имеющего тенденции.

Соответственно различают модели Брауна:

­ нулевого порядка, которая описывает процессы, не имеющие тенденции развития. Она содержит один параметр А₀;

­первого порядка 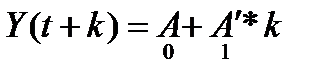, отражающей тенденцию в виде прямой линии;

­ второго порядка, отражающей развитие в виде параболической тенденции с «ускорением». Прогноз осуществляется по формуле: .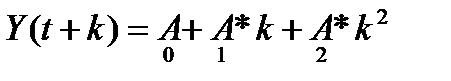

Порядок модели определяют обычно либо априорно на основе визуального анализа графика процесса, либо методом проб, сравнивая статистические характеристики моделей различного порядка на участке прогнозирования.

Рассмотрим этапы построения линейной модели Брауна:

Этап 1. По первым пяти точкам временного ряда оцениваются начальные значения А₀ и A₁ с помощью МНК:

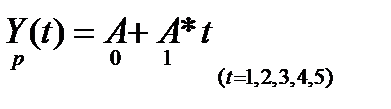
Этап 2. С использованием полученного уравнения рассчитывают прогноз на один шаг (к=1)

.

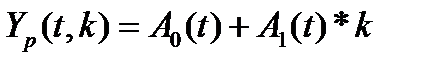Этап 3. Вычисляется величина расхождения расчетного значения с фактическим :

,

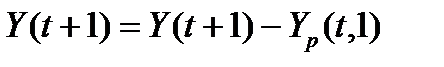где Y(t+1) – фактическое значение экономического показателя.

Этап 4. В соответствии с этой величиной корректируются параметры модели.

Этап 5. По модели со скорректированными параметрами A₀ и A₁ находят прогноз на следующий момент времени. Если t<N, то возврат на пункт 3 если t=N, то модель можно использовать для прогнозирования.

Этап 6. Строится интервальный прогноз.

В авторегрессионых моделях текущее значение процесса представляется как линейная комбинация предыдущих его значений и случайной компоненты.

53. Компоненты временного ряда

Временной ряд — это совокупность значений какого-либо по­казателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

• факторы, формирующие тенденцию ряда;

• факторы, формирующие циклические колебания ряда;

• случайные факторы.

При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство времен­ных рядов экономических показателей имеют тенденцию, харак­теризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправ­ленное воздействие на исследуемый показатель. Однако в сово­купности они формируют его возрастающую или убывающую тенденцию. Рис1

Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезон­ный характер, поскольку экономическая деятельность ряда от­раслей экономики зависит от времени года рис2 Некоторые временные ряды не содержат тенденции и цикли­ческой компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Рис3

В большинстве случаев фактический уровень временного ря­да можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой вре­менной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в ко­торой временной ряд представлен как произведение перечислен­ных компонент, называется мультипликативной моделью времен­ного ряда. Основная задача эконометрического исследования от дельного временного ряда — выявление и придание количествен­ного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогно­зирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

54. Метод проверки гипотез о существовании тренда во временном ряду, основанный на сравнении средних уровней ряда

Сущность всех методов исключения тенденции заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда. Основные методы исклю­чения тенденции можно разделить на две группы:

• методы, основанные на преобразовании уровней исходного
ряда в новые переменные, не содержащие тенденции. Полу­ченные переменные используются далее для анализа взаимо­связи изучаемых временных рядов. Эти методы предполага­ют непосредственное устранение трендовой компоненты Т из каждого уровня временного ряда. Два основных метода в
данной группе — это метод последовательных разностей и
метод отклонений от трендов;

• методы, основанные на изучении взаимосвязи исходных
уровней временных рядов при элиминировании воздействия
фактора времени на зависимую и независимые переменные
модели. В первую очередь это метод включения в модель рег­рессии по временным рядам фактора времени.
Рассмотрим подробнее методику применения, преимущества и недостатки каждого из перечисленных выше методов. Метод отклонений от тренда

Пусть имеются два временных ряда x_t и y_t каждый из которых содержит трендовую компоненту Т и случайную компоненту е. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни 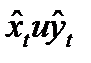соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. 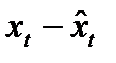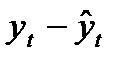Дальнейший анализ взаимосвязи ря­дов проводят с использованием не исходных уровней, а отклонений от тренда и при условии, что последние не содержат тенденции.

В ряде случаев вместо аналитического выравнивания времен­ного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.

Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями).

Пусть (1) 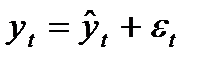; 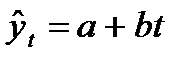(65.1)

Тогда 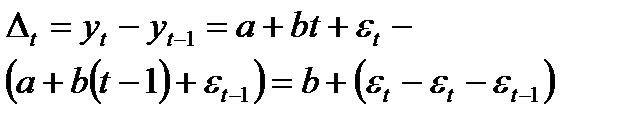(65.2)

Тогда

Коэффициент b — константа, которая не зависит от времени.

Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.

Пусть имеет место соотношение (1), однако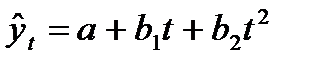

Тогда 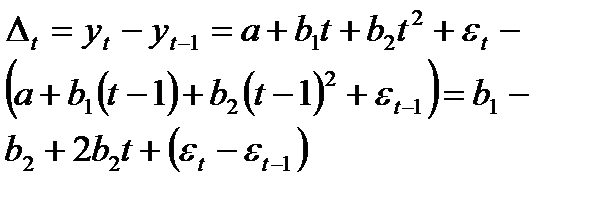(65.3)

Как показывает это соотношение, первые разности ∆_t , непо­средственно зависят от фактора времени t и, следовательно, со­держат тенденцию.

Определим вторые разности:

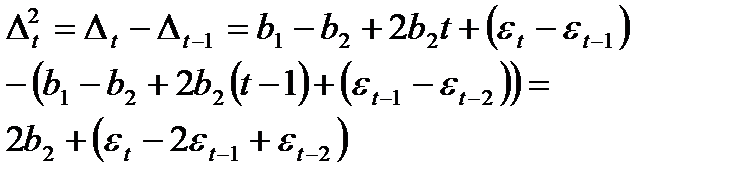(65.4)

Очевидно, что вторые разности ∆_t², не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме пара­болы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствует экспо­ненциальный или степенной тренд, метод последовательных раз­ностей следует применять не к исходным уровням ряда, а к их ло­гарифмам.

55. Метод Чоу проверки стабильности тенденций. Особенности применения теста Чоу.

1. Если число параметров во всех уравнениях из таблицы 3 (1), (2), (3) одинаково и равно k, то формула (56) упрощается:

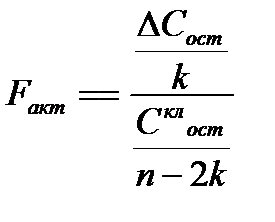(66.1)

2. Тест Чоу позволяет сделать вывод о наличии или отсутствии структурной стабильности в изучаемом временном ряде. Если F_факт < F_табл , то это означает, что уравнения (1) и (2) описывают одну и ту же тенденцию, а различия численных оценок их пара метров а₁ и а₂ , а также b₁ и b₂ соответственно статистически не значимы. Если же F_факт > F_табл то гипотеза о структурной стабильности отклоняется, что означает статистическую значимость различий в оценках параметров уравнений (1) и (2).

З. Применение теста Чоу предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях (1) и (2) и независимость их распределений.

Если гипотеза о структурной стабильности тенденции ряда у, отклоняется, дальнейший анализ может заключаться в, исследовании вопроса о причинах этих структурных различий и более де 1 изучении характера изменения тенденции. В принятых обозначениях эти причины обусловливают различия в оценках параметров уравнений (1) и (2).

Возможны следующие сочетания изменений числейных оценок параметров этих уравнений :

• Изменение численной оценки свободного члена уравнения Тренда а₂ по сравнению с а₁ при условии, что различия b₁ и b₂ статистически незначимы. Геометрически это означает, что прямые (1) (2) параллельны. Происходит скачкообразное изменение уровня ряда у_t, в момент времени t‚ и неизменном среднем абсолютном приросте за период;

• Изменение численной оценки параметра b₂ по сравнению с b₁ при условии, что различия между а₁ и а₂ статистически незначимы. Геометрически это означает, что прямые (1) и (2) пересекают ось координат в одной точке. Изменение тенденции происходит посредством изменение среднего абсолютного прироста временного ряда, начиная с момента времени t‚ при неизменном начальном уровне ряда в момент времени t =0

• Изменение численных оценок параметров а₁ и а₂, а так же b₁ и b₂ . На графике это отображается изменением начального уровня и счреднего за период абсолютного прироста

56. Аналитический вид тренда

Одним из наиболее распространенных способов моделирова­ния тенденции временного ряда является построение аналитиче­ской функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим вы­равниванием временного ряда.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные ви­ды функций. Для построения трендов чаще всего применяются следующие функции:

• линейный тренд: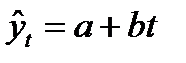

• гипербола: ,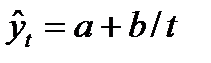

• экспоненциальный тренд: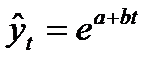

• тренд в форме степенной функции: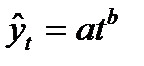

• парабола второго и более высоких порядков: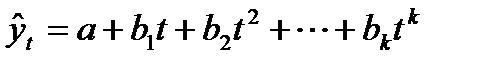

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой перемен- 1 ной — фактические уровни временного ряда y_t . Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэф­фициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни у_t и у_t-1 тес­но коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, напри­мер, в форме экспоненты, то коэффициент автокорреляции пер­вого порядка по логарифмам уровней исходного ряда будет вы­ше, чем соответствующий коэффициент, рассчитанный по уров­ням ряда. Чем сильнее выражена нелинейная тенденция в изуча­емом временно м ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит не­линейную тенденцию, можно осуществить путем перебора ос­новных форм тренда, расчета по каждому уравнению скорректи­рованного коэффициента детерминации R² и выбора уравнения тренда с максимальным значением скорректированного коэффи­циента детерминации.