Рассмотрим мультипликативную производственную функцию

X=A* K^α₁*L ^α₂, ^α₁>0, >0 (68.2)

где А – коэффициент нейтрального технического прогресса; ^α₁,^α₂ - коэффициенты эластичности по труду и фондам.

Частным случаем этой функции является известная функция Кобба- Дугласа:

X =A*K ^α*L ^1-α , ^α₁= ^α, ^α₂= ^{1- α} . (68.3)

Логарифмируя эту функцию, получаем

Ln X =Ln A +α *ln K +(1- α)*ln L ,

т.е. в логарифмах функции (68.3) и (68.2) линейны и являются моделями множественной регрессии, где параметры А, ^α₁, могут быть определены по методу наименьших квадратов.

Можно показать (доказать), что производственная функция (68.2) является неоклассической, т.е. отвечает вышеперечисленным условиям 1-4.

Производственная функция называется однородной степени r, если,

F (λ * K, λ * L) = λ^γ * F (K, L) . Класс производственных функций с постоянной эластичностью замены, называется СES – функциями:

где .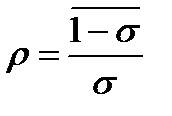

При λ =1; σ→1 (p→0) СES – функция стремится к функции Кобба-Дугласа.

При p→ -1, γ=1 СES – функция переходит в линейную ПФ:.

Разработкой макроэконометрических моделей занимался Л.Клейн. По Клейну, такие макроэкономические показатели, как валовой национальный продукт, расходы федерального правительства, ставка процента и цены, являются «движущей силой» региональных моделей.

В 1950 г. Л. Клейн предложил динамическую модель макроэкономики, (получившую название модель Клейна1.) систему уравнений:

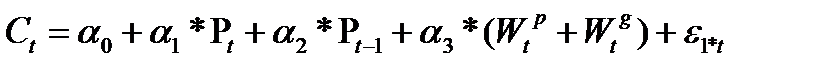- потребление,

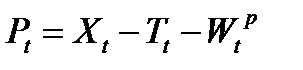- доход частного сектора,

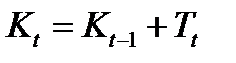- капитал.

Переменные, стоящие в левых частях уравнений, являются эндогенными.

58. Сезонная корректировка: основные идеи и термины

Общая модель. Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается S_t, где t обозначает момент времени), (2) тренда (T_t), (3) циклической компоненты (C_t) и (4) случайной, нерегулярной компоненты или флуктуации (I_t). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TC_t). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:

Аддитивная модель:

X_t = TC_t + S_t + I_t

Мультипликативная модель:

X_t = T_t*C_t*S_t*I_t

Здесь X_t обозначает значение временного ряда в момент времени t.

Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд.)

Аддитивная и мультипликативная сезонность.Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1.4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным. Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1.4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.

59. Сезонные фиктивные переменные

Одно из условий, на которое опирается эконометрическое моделирование состоит в том, что функциональное соотношение не меняется в течении рассматриваемого периода. Однако это условие часто нереалистично, особенно в случае, когда приходится иметь дело с переходной экономикой. Это обычная проблема, с которой экономист сталкивается при исследовании экономических процессов с изменчивой структурой. Как бы то ни было, приходится делать предположение о неизменности формы модели, иначе моделирование не было бы возможно.

Один из возможных способов учета структурных сдвигов состоит в использовании различного рода сконструированных переменных, таких как, фиктивные переменные и тренды. Включение в эконометрическую модель трендов позволяет учитывать изменения во всех коэффициентах регрессионного уравнения: свободном члене и коэффициентах при “экономических” переменных. Фиктивные переменные (принимающие только два значения — 0 и 1) позволяют учесть резкие структурные скачки.

Кроме того, использование фиктивных переменных и гармонических трендов (синусов и косинусов) позволяет учесть в модели сезонные колебания. Если предположить, что сезонность имеет детерминированный характер, то ее можно смоделировать, добавив в уравнение регрессии компоненту следующего вида:

d ₁ M₁ + ... + d ₁₂ M₁₂.

Здесь M₁, ..., M₁₂ — сезонные месячные переменные.

Все же эти методы не позволяют адекватно учесть изменения, если неизвестен их характер или момент изменения (в случае скачка). Особенно большие проблемы создают структурные сдвиги для прогнозирования. Если резкое изменение в параметрах экономического процесса произошло в течение исследуемого периода, то это изменение можно заметить и учесть в модели. Если же неожиданное изменение произойдет после исследуемого периода, то сделанные прогнозы окажутся неверными.