Сущность и особенности региональных эконометрических моделей

Региональные эконометрические модели (РЭМ) представляют собой системы регрессионных уравнений (или отдельные уравнения), связывающие экзогенные и эндогенные переменные, выражающие экономические показатели регионального уровня. Выбор математической формы зависимости и оценка параметров эконометрических моделей осуществляется с помощью методов математической статистики на основе информации временных рядов. Успех в использовании эконометрических моделей в прогнозировании и регулировании экономических процессов зависит от динамики изучаемых процессов (когда изучаемые процессы не претерпевают резких, скачкообразных изменений).

Выделяются два типа регрессионных РЭМ:

* простые, состоящие их одного или не связанных между собой уравнений;

* состоящие из системы совместных уравнений, решение которой определяет - систему эндогенных переменных.

Уравнение простой эконометрической модели имеет вид:

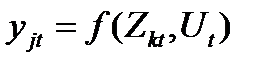(75.1)

где 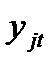- j-я эндогенная переменная в момент времени t, выражающая результативный экономический показатель;

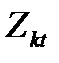- k-я экзогенная переменная в момент времени t, показатель-фактор;

- ошибка наблюдений в момент времени t.

Простые эконометрические модели, построенные для различных регионов, могут существенно отличаются друг от друга, что свидетельствует о том, что итоговые экономические показатели различных регионов по-разному реагируют на изменения показателей факторов.

В моделях с совместными уравнениями каждое уравнение включает эндогенные переменные y_i (j=1,…,n), экзогенные переменные Z_k (k=1,…,I) и случайные переменные U_i (i=1,…,n). Система уравнений для момента времени t имеет вид:

i=1,…,n; t=1,…,T. (6.7)

В матрично-векторных обозначениях эта система записывается следующим образом:

B*Y_t+C*Z_t=U_t

, (75.2)

где Y_t - n-мерный вектор эндогенных переменных в момент t;

Z_t- I- мерный вектор экзогенных переменных (включая эндогенные переменные с лагом) в момент t;

U_t - n-мерный вектор случайных составляющих в момент t;

В - матрица коэффициентов при эндогенных переменных размера ;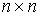

C - матрица коэффициентов при экзогенных переменных, размера .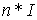

Редуцированная форма линейной модели может быть получена в случае, если В – неособенная матрица:

Y_t = - B^-1 * C * Z_t+ B^-1 * U_t . 75.3

В построении РЭМ основным препятствием является недостаточное число наблюдений для выбора наиболее значимых зависимостей и оценки параметров.

Это объясняется меньшей полнотой и системностью региональной статистики и более короткими временными рядами данных в разрезе регионов. Российская статистика в настоящее время завершает переход на международный стандарт Системы национальных счетов (СНС), однако этот процесс на региональном уровне находится еще на начальной стадии. Это затрудняет информационное обеспечение РЭМ-ей, вынуждает ограничиваться построением моделей, наименее требовательных к исходной информации.

63. Вероятность. Случайная величина

Любая деятельность в экономике по своей сути является вероятностной, то есть вероятностным экспериментом.

Событие – это любой исход, какого – либо вероятностного эксперимента.

Вероятность события А - это отношение числа m исходов, благоприятствующих появлению данного события, к общему числу n исходов, данного вероятностного эксперимента

P(A) =m/n

(76.1)

Из определения вытекает очевидное неравенство

0 ≤ P(A) ≤ 1

Случайная величина (СВ) – это величина, которая может принимать то или иное значение, из некоторого множества значений.

Спрос на какую – либо продукцию, прибыль фирмы, объем экспорта за определенное время и т. д. являются случайными величинами.

Различают дискретные и непрерывные СВ. Дискретной называют такую СВ, которая принимает отдельные, изолированные значения с определенными вероятностями. Например, число покупателей в магазине в определенный момент времени, количество определенного товара, продаваемого ежедневно в магазине, число автомобилей на проспекте и т. д. является дискретными СВ. Непрерывной называется случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного числового промежутка. Большинство СВ, рассматриваемых в экономике, имеют настолько большое число возможных значений, что их удобнее представлять в виде непрерывных СВ. Например, курсы валют, доход, объемы ВНП, ВВП и т. д.

Для описания дискретной СВ необходимо установить соответствие между всевозможными значениями СВ и их вероятностями. Такое соответствие называется законом распределения дискретной СВ. Его можно задать таблично, аналитически (в виде формулы) либо графически.

Например, табличное задание закона распределения дискретной СВ:

где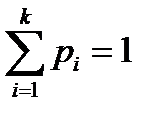

налитически СВ задается либо функцией распределения, либо плотностью вероятностей.

Функцией распределения СВ Х называется функция F(x), которая определяется следующим образом: F(x) =P(X<x)

то есть это есть вероятность того, что СВ Х принимает значение меньшее, чем х.

Отметим некоторые свойства F(x):

1) 0 ≤ F(x) ≤ 1

2) F(x) - неубывающая функция, то есть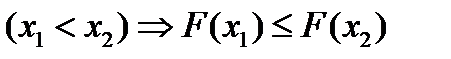

3)

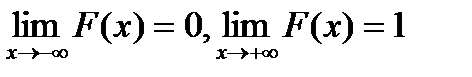
4) Если СВ Х принимает значения из отрезка [a,b], то

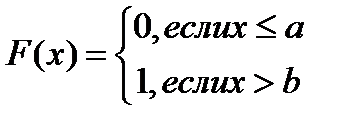
5)

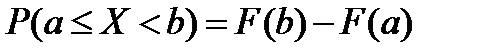
Плотностью вероятности (плотностью распределения вероятностей) непрерывной СВ Х называют функцию