Нормальное распределение. Нормальное распределение (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности.

Нормальное распределение (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности.

Говорят, что СВ Х имеет нормальное распределение, если ее плотность вероятности имеет вид:

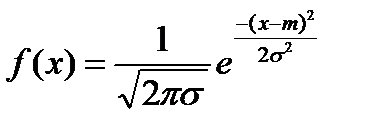(78.1)

Откуда получаем, что

(78.2)

Как видно из формул (1.9) и (1.10) нормальное распределение зависит от параметров m и s. При этом

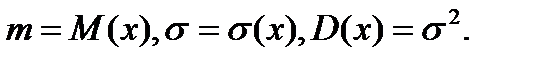
Если СВ Х имеет нормальное распределение с параметрами m и s, то символически это записывается так:

X~N(m,s) или X~N(m, s²)

В случае, когда m=0 и s =1 говорят о стандартном нормальном распределении.

Распределение c² (хи – квадрат)

Пусть х_i (i=1,2,…,n) -независимые нормально рас предельные СВ с математическими ожиданиями m_i и среднеквадратическими отклонениями si, соответственно, то есть х_i~N(m_i,si).

Тогда СВ 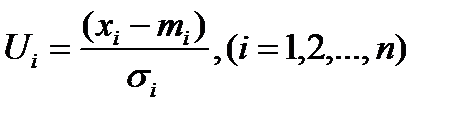являются независимыми СВ, имеющими стандартное нормальное распределение, U_i~N(0,1).

Случайная величина c² имеет хи – квадрат распределение с n- степенями свободы (c²~c²_n), если

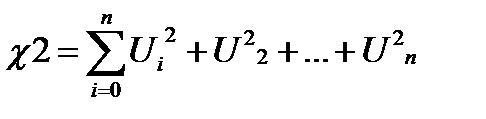(78.3)

(Число степеней свободы СВ определяется числом СВ, ее составляющих , уменьшенным на число линейных связей между ними ).

Распределение c² определяется одним параметром - числом степеней свободы J.

M(c² )=J; D(c²) =2J.