Недостаточный набор данных

Имеющихся данных может быть недостаточно для того, чтобы определить функциональную связь между переменными, либо они недостаточно варьируются, чтобы можно было отличить влияние одного фактора от влияния другого. Последняя проблема получила в эконометрическом моделировании название “мультиколлинеарности”. В отличие от экспериментальных наук, у отдельного исследователя, изучающего экономические процессы, как правило, нет возможности сколько-нибудь заметно на них повлиять. Обычно за него это делает правительство. “ ...От правительственного манипулирования экономикой могла бы выиграть только эконометрика.”.

Чтобы восполнить недостаток данных, исследователю приходится делать некоторые априорные допущения, зачастую недостаточно обоснованные.

60. Автокорреляция уровней временного ряда. Анализ структуры временного ряда на основании коэффициентов автокорреляции

Корреляционную зависимость между последова­тельными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного ко­эффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид: 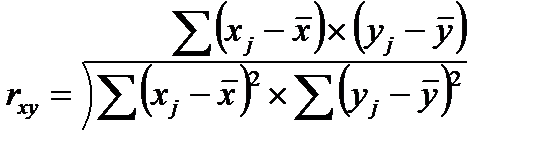(73.1)

можно определить коэффициенты автокорреля­ции второго и более высоких порядков. Так, коэффициент авто­корреляции второго порядка характеризует тесноту связи между уровнями у_t и y_t-1 и определяется по формуле:

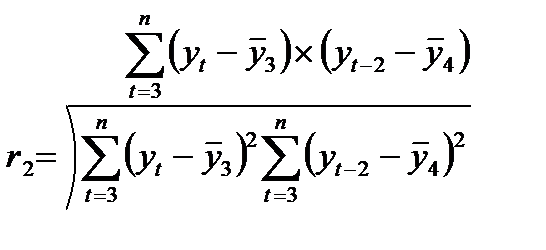(73.2)

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорре­ляции, уменьшается.

Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда.

Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уров­нях ряда.

Последовательность коэффициентов автокорреляции уров­ней первого, второго и т. д. порядков называют автокорреляцион­ной функцией временного ряда. График зависимости ее значений от величины лага на­зывается коррелограммой.

61. Модели стационарных и нестационарных временных рядов.

Пусть 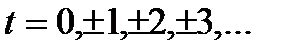Рассмотрим временной ряд X(t). Пусть сначала временной ряд принимает числовые значения. Это могут быть, например, цены на батон хлеба в соседнем магазине или курс обмена доллара на рубли в ближайшем обменном пункте. Обычно в поведении временного ряда выявляют две основные тенденции - тренд и периодические колебания.

При этом под трендом понимают зависимость от времени линейного, квадратичного или иного типа, которую выявляют тем или иным способом сглаживания (например, экспоненциального сглаживания) либо расчетным путем, в частности, с помощью метода наименьших квадратов. Другими словами, тренд - это очищенная от случайностей основная тенденция временного ряда.

Временной ряд обычно колеблется вокруг тренда, причем отклонения от тренда часто обнаруживают правильность. Часто это связано с естественной или назначенной периодичностью, например, сезонной или недельной, месячной или квартальной (например, в соответствии с графиками выплаты заплаты и уплаты налогов). Иногда наличие периодичности и тем более ее причины неясны, и задача эконометрика - выяснить, действительно ли имеется периодичность.

Характеристики временных рядов. Для более подробного изучения временных рядов используются вероятностно-статистические модели. При этом временной ряд X(t) рассматривается как случайный процесс (с дискретным временем) основными характеристиками являются математическое ожидание X(t), т.е.

,

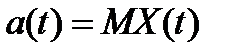дисперсия X(t), т.е.

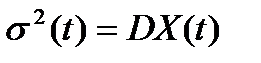
и автокорреляционная функция временного ряда X(t)

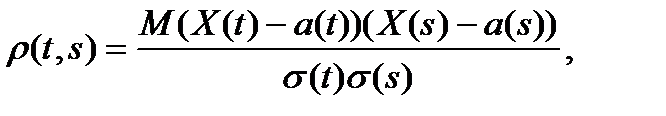
т.е. функция двух переменных, равная коэффициенту корреляции между двумя значениями временного ряда X(t) и X(s).

В теоретических и прикладных исследованиях рассматривают широкий спектр моделей временных рядов. Выделим сначала стационарные модели. В них совместные функции распределения 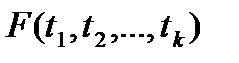для любого числа моментов времени k, а потому и все перечисленные выше характеристики временного ряда не меняются со временем. В частности, математическое ожидание и дисперсия являются постоянными величинами, автокорреляционная функция зависит только от разности t-s. Временные ряды, не являющиеся стационарными, называются нестационарными.

Линейные регрессионные модели с гомоскедастичными и гетероскедастичными, независимыми и автокоррелированными остатками. Как видно из сказанного выше, основное - это "очистка" временного ряда от случайных отклонений, т.е. оценивание математического ожидания. В отличие от простейших моделей регрессионного анализа, рассмотренных в главе 5, здесь естественным образом появляются более сложные модели. Например, дисперсия может зависеть от времени. Такие модели называют гетероскедастичными, а те, в которых нет зависимости от времени - гомоскедастичными. (Точнее говоря, эти термины могут относиться не только к переменной "время", но и к другим переменным.)

Далее, в главе 5 предполагалось, что погрешности независимы между собой. В терминах настоящей главы это означало бы, что автокорреляционная функция должна быть вырожденной - равняться 1 при равенстве аргументов и 0 при их неравенстве. Ясно, что для реальных временных рядов так бывает отнюдь не всегда. Если естественный ход изменений наблюдаемого процесса является достаточно быстрым по сравнению с интервалом между последовательными наблюдениями, то можно ожидать "затухания" автокорреляции" и получения практически независимых остатков, в противном случае остатки будут автокоррелированы.