Виды нелинейностей характеристик нелинейных элементов

На рис.58 приведены характерные нелинейные характеристики нелинейных элементов, связывающие значения сигнала y на выходе элемента с сигналом x на его входе.

На рис.58а приведена характеристика усилителя-ограничителя с зоной линейности. При значениях входного сигнала 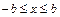выходной сигнал y=kx, где 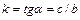, то есть выходной сигнал прямопропорционален входному сигналу. При 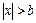выходной сигнал 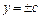, т.е. имеет место режим ограничения.

На рис.58б приведена нелинейная характеристика треугольной формы с зоной линейности при .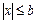

На рис.58в приведена характеристика идеального ограничителя. Такую характеристику называют иногда релейной. Сигнал на выходе идеального ограничителя y=c при и y=-c при .

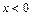На рис.58г приведена характеристика, в которой зона линейности плавно переходит в зону ограничения. Такими свойствами обладают функции y=arctgx, y=thx и некоторые другие. Такие характеристики имеют дифференциальные усилительные каскады.

На рис.58д приведена характеристика вида y=csinx. Такими характеристиками обладают некоторые фазовые и частотные детекторы.

На рис.58е приведена характеристика ограничителя с гистерезисом. Такой характеристикой обладают двухпозиционные поляризованные реле. В характеристиках с гистерезисом зависимость y=f(x) происходит по разному в зависимости от того, в какую сторону изменяется входной сигнал x.

На рис.58ж приведена характеристика, аналогичная той, что приведена на рис.10.1.г, но с гистерезисом.

На рис.58з приведена характеристика ограничителя с зоной нечувствительности. В этом ограничителе выходной сигнал y=0 при 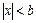, а при 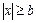выходной сигнал .

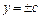На рис.58и приведена характеристика ограничителя с зоной нечувствительности и с гистерезисом. Такими характеристиками обладают трехпозиционные поляризованные реле или реле с нейтралью.

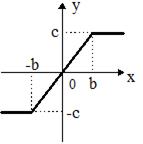
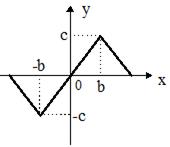
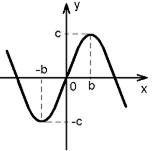
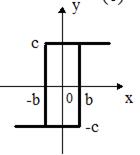
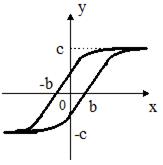
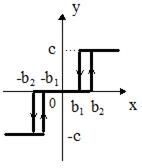
Рис.58 Характеристики нелинейных элементов