Описание САУ (ЦСУ) в пространстве состояний. Соотношения для коэффициентов.

Дифференциальное уравнение 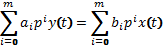можно представить в виде системы из m дифференциальных уравнений первого порядка. Для этого введем промежуточные переменные g_i(t), которые называют переменными состояния системы.

Без нарушения общности примем в 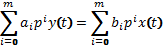коэффициент а_m=1 и перепишем это уравнение в виде

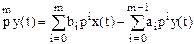
Математик Коши доказал, что этому уравнению эквивалентна следующая система уравнений:

y(t) = g₁(t) + В₀ (t), (1)

где 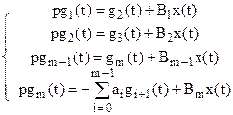(2)

здесь 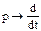- символ дифференцирования.

Эквивалентность (1) и (2) дифференциальному уравнению обеспечивается при выполнении определенных соотношений между коэффициентами а_i, b_i и B_i. Например, при порядке системы m=3 эти соотношения имеют вид:

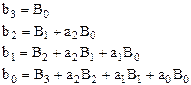
откуда:

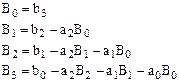
При m=4 имеем соответственно:

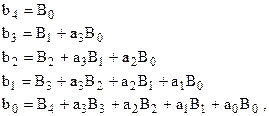
откуда легко получить выражение для коэффициентов В_i.

Из этих формул легко просматривается общая закономерность получения соотношений между а_i, b_i и B_i при любом порядке системы m.