Применение метода гармонической линеаризации для анализа нелинейных САУ.

На рис.59 приведена схема нелинейной системы, для анализа которой можно воспользоваться методом гармонической линеаризации

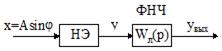
Рис.59 Структурная схема нелинейной системы

В этой схеме входной сигнал 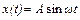- гармонический, а после нелинейного элемента НЭ включен фильтр нижних частот (ФНЧ) с передаточной функцией .

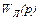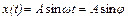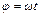При гармоническом входном сигнале , где сигнал y на выходе НЭ будет периодическим, но не гармоническим, так как зависимость y=f(x) нелинейная. Периодические сигналы можно представить рядом Фурье

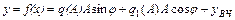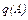, где и 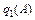- коэффициенты ряда Фурье для первых гармоник синуса и косинуса, которые определяются по формулам: 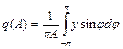, , 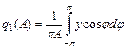где y - сигнал на выходе НЭ при изменении фазы j входного сигнала x от - 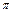до 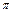, 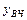- высокочастотные составляющие (высшие гармоники) в сигнале y.

Так как на выходе НЭ включен фильтр нижних частот, который не пропускает на выход высшие гармоники сигнала y, тогда на его выходе будут присутствовать только первые гармоники в сигнале y, т. е. .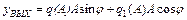

Так как 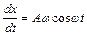, откуда 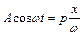, здесь - символ дифференцирования.

Следовательно, .

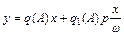От гармонических сигналов x и y перейдем к комплексным сигналам путем замены , тогда получим:

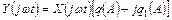
Это соотношение устанавливает связь между первой гармоникой комплексных сигналов на входе и выходе НЭ, для которого введем понятие нелинейного ККП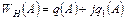

тогда .

Определим коэффициенты 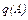и 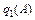для нелинейных элементов, характеристики которых приведены на рис.58в и 58з.

Для идеального ограничителя (рис.58в) получим:

= = = ;

= .

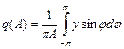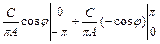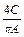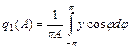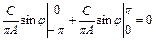Для ограничителя с зоной нечувствительности получим

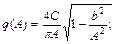
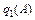=0.

Отметим, что для всех симметричных характеристик без гистерезиса 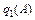=0.

В таблице приведены выражения для расчета коэффициентов 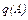и 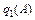наиболее характерных НЭ, характеристики которых приведены на рис.58.