Применение критерия Найквиста и метода гармонической линеаризации для определения устойчивости и параметров автоколебаний в нелинейных САУ.

На рис.10.3 приведена структурная схема замкнутой нелинейной системы, где заштрихованный сектор в сумматоре соответствует умножению на -1.

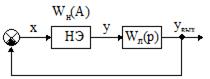
Рис.10.3 Структурная схема замкнутой нелинейной системы

Для проверки устойчивости этой системы воспользуемся критерием Найквиста, по которому автоколебания в системе возникнут, если годограф разомкнутой системы охватит на комплексной плоскости точку с координатами - 1; j 0.

Для разомкнутой схемы на рис.10.3 имеем

, где .

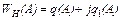Условия возникновения автоколебаний в замкнутой системе по критерию Найквиста математически можно записать так: 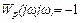, или 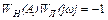, откуда 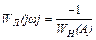(10.5)

Это комплексное уравнение устанавливает возможность возникновения автоколебаний в системе на рис.10.3 и позволяет определить параметры - амплитуду 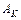и частоту 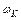этих колебаний /13/.

На рис.10.4 приведено графическое уравнение (10.5) в двух случаях: когда решение единственное (рис.10.4.а) и когда есть две точки решения (рис.10.4.б).

Во втором случае установившимся будет решение в точке 2, так как этой точке соответствует большая амплитуда колебаний .

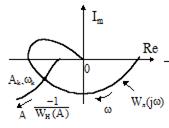
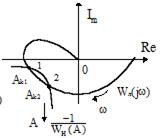
Рис.10.4 Графическое решение уравнения (10.5)

Рассмотрим примеры построения годографа 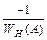для нелинейных элементов, характеристики которых приведены на рис.10.1.в и 10.1.з.

Для идеального ограничителя (рис.10.1.в) имеем , .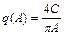

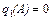Тогда .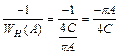

Этот годограф приведен на рис.10.5.а. Он идет от нуля в - 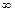по действительной оси. Отметим, что с идеальным ограничителем в замкнутой системе автоколебания возникнут всегда, если годограф линейной части системы 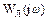пересекает отрицательную действительную ось. Коэффициент усиления не играет роли, так как у идеального ограничителя .

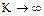Для ограничителя с зоной нечувствительности имеем

.

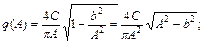
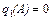Тогда годограф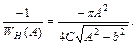

При 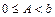он идет по мнимой оси от нуля до 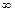, а при 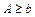он идет по действительной оси из - 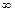в точку с координатой 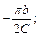j0, а затем из этой точки снова уходит в + 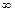. График этого годографа приведен на рис.10.5.б /5, 12/.

Из этого рисунка видно, что для возникновения автоколебаний в замкнутой системе с ограничителем с зоной нечувствительности (рис.10.1.з) годограф линейной части системы должен пересечь отрицательную действительную ось левее точки с координатами 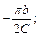j0. На рис.10.5.б этой ситуации соответствует годограф .

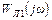Иначе говоря, коэффициент усиления линейной части системы на критической частоте должен быть больше величины 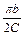. В противном случае автоколебаний в системе не будет. На рис.10.5.б этой ситуации соответствует годограф .

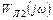(а)

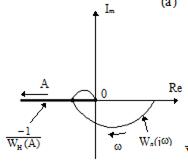
(б)

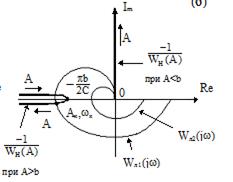
Рис.10.5 Годографы 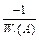идеального (а) и неидеального (б) ограничителей