ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУПП. ТЕРМИНОЛОГИЯ

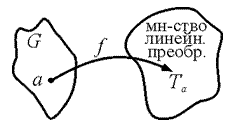Def: Линейным представлением группы G в конечномерном евклидовом пространстве Еⁿ называется такое отображение f, посредством которого "aÎG $T_a – линейный оператор пространства Еⁿ так, что "a₁, a₂ÎG выполнено соотношение: T(a₁, a₂) = 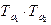. Т.е. осуществляет гомоморфизм группы G на некоторое подмножество линейных преобразований.

Используется следующая терминология: Еⁿ – пространство представления; dimЕⁿ – размерность представления; базис в Еⁿ – базис представления.

Сам гомоморфный образ f(G) группы G также называется представлением группы G в пространстве представлений.

В дальнейшем: n-мерное линейное представление группы будем называть (для кратности) представлением этой группы.

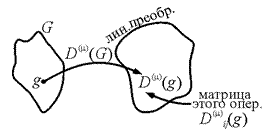Обозначениепредставления группы : D(G).

Различные представления группы : D^(m)(G).

D^(m)(y) – это линейный оператор: f: g ® D^(m)(y).

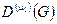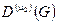Представления и группы G в одном и том же пространстве называются эквивалентными, если $С – линейный оператор в Еⁿ такой, что

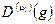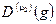"gÎG: = C^–1 С.

Тривиальное представление группы G: гомоморфизм G на единичный элемент группы GL(n).

Если f: G ® G₁, где G₁ подгруппа в GL(n) и если f – изоморфизм, то представление называется точным. (Не у всякой группы есть точное n-мерное представление для заданного n).

Например: У О(10) нет точного одномерного представления: группа О(1) – абелева, а группа О(10) не абелева.