Билинейные функционалы

Функционал j(х, у) называется симметричным, если j(х, y) = j(y, х). (При этом j(e_i, e_j) = j(e_j, e_i) т.е. u_ij = u_ji).

Функционал j(х, y) называется антисимметричным, если j(х, y) = –j(y, х) (При этом j(e_i, e_j) = – j(e_j, e_i) т.е. u_ij = –u_ji).

Если в заданной билинейной форме j(х, y) положить х = у, то получим частный случай билинейной формы – квадратичную форму.

2°. Любой билинейный функционал можно представить в виде суммы симметричного и антисимметричного функционалов.

◀ j_s(х, y) = (j(х, у) + j(y, х))/2, j_А(х, y) = (j(х, у) – j(y, х))/2. ▶

3°. Каждому билинейному симметричному функционалу (билинейной форме) можно поставить в соответствие квадратичную форму и наоборот.

◀ *) j(х, y) = j(y, х) Û j(х, х);

**) j(х + y, х + у) = j(х, х) + j(х, y) + j(y, х) + j(у, у) = j(х, х) + 2j(y, х) + j(у, у) Þ

Þ j(х, у) = 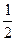[j(х + y, х + у) – j(х, х) – j(у, у)]. ▶

4°. Если билинейный функционал антисимметричен, то соответствующая ему квадратичная форма равна нулю.

◀ j(х, y) = –j(y, х). Полагая в данном равенстве y=x получим j(х, х) = –j(х, х) = 0. ▶