Линейный функционал
Пусть Vn – n-мерное линейное пространство. Если для любого хÎVn существует число j(х)ÎК, где К некоторое числовое поле, то говорят, что на пространстве Vn задан функционал φ со значениями в поле К.
Функционал j(х) называется линейным функционалом, если
а) "х, уÎVn j(х + у) = j(х) + j(у) (аддитивность);
б) "хÎVn "aÎК j(aх) = aj(х) (однородность).
Пусть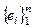 
базис в Vn. Тогда "хÎVn: х = 
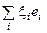Þ j(х) = j 
= 
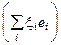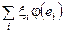. Таким образом, чтобы задать линейный функционал в линейном пространстве, достаточно задать величины ui = j(ei), т.е. каждому линейному функционалу можно поставить в соответствие вектор u = (u1, u2, … , un) такой, что j(х) = (x, u) = 
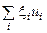. Действие функционала j на вектор х можно трактовать и как умножение матриц j(х) = (u1, u2, … , un)(ξ1, ξ2, … , ξn)Т.
Запись линейного функционала в некотором базисе в виде j(х) =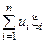 
называется линейной формой. Таким образом, линейная форма это запись линейного функционала в некотором базисе.
§2. Пространство линейных функционалов на Vn
Рассмотрим множество возможных линейных функционалов на Vn. Два функционала f и j будем называть равными, если "хÎVn f(x) = j(х).
Введем операции сложения функционалов и умножение функционалов на скаляр из вещественного поля K так:
a) g = f + j Û "хÎVn g(x) = f(x) + j(х);
b) g = lf Û "хÎVn, "lÎK g(x) = lf(x).
Нетрудно убедится, что множество линейных функционалов с так введенными операциями образуют линейное пространство. В качестве нейтрального функционала q определим функционал, который "хÎVn q(х) = 0. Построенное таким образом пространство линейных функционалов заданных на Vn, называется пространством, сопряженным к Vn и обозначается Vn*.
1°. dimVn = dimVn*. ◀ ▶
Дата добавления: 2015-05-05; просмотров: 689;