И сходимость по норме

Далее рассмотрим нормированное линейное пространство с метрикой r(х, у) = ||х – у||.

Сходимость последовательности векторов в такой метрике называется сходимостью по норме.

В вещественном и комплексном конечномерном пространстве, кроме сходимости по норме можно ввести другое понятие сходимости. Для любой последовательности {х_m} векторов из Х запишем разложение векторов х_m по базису {e_k}: 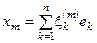. Пусть .

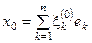Def: Если "k =1, 2, …, n имеет место 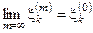, то говорят, что имеет место покоординатная сходимость последовательности {х_m}® х_{0 .}

Координатная сходимость в линейном пространстве является естественной в том смысле, что если два вектора близки, то естественно предположить, что и координаты их близки.

Соответственно, аналогично, естественной сходимостью в нормированном (или метрическом) пространстве является сходимость по норме (или по метрике).