Полнота метрических пространств

Последовательность 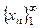ÎХ называется фундаментальной или сходящейся в себе, если "e > 0 $N ½"n, m > N r(х_n, х_m) < e.

4°. Любая фундаментальная последовательность ограничена.

◀ e₀ > 0 $N₀½"m > N r(х_m, 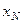) < e₀. Тогда все элементы последовательности 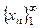принадлежат шару с центром х₀ и радиуса z₀ = max{e₀, r(х₁, 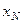), … , r( , )}. ▶

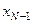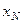5°. Если последовательность сходится, то она фундаментальна.

◀ Пусть 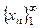® х₀. Тогда "e > 0 $N "n > N r(х_n, x₀) < e/2. Кроме того,

r(х_n, x_m) £ r(х_n, x₀) + r(х₀, x_m) < e "n, m > N. ▶

Для множества вещественных чисел справедливо и обратное утверждение: любая фундаментальная последовательность – сходится.

В общем случае это не так. Подтверждением этого служит факт, что последовательность рациональных чисел не обязательно сходится к рациональному числу.

Def: Метрическое пространство называется полным если любая фундаментальная последовательность в нем сходится к элементу этого же метрического пространства.

В каждом метрическом пространстве имеет место теорема – аналогичная теореме о вложенных сегментах для действительных чисел.

6°. Пусть в полном метрическом пространстве Х задана последовательность 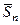(a_n, e_n) замкнутых шаров, вложенных друг в друга, т.е. 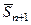(a_n+1, e_n+1) Ì 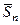(a_n, e_n) "nÎN.

Если последовательность радиусов e_n ® 0 , то существует и единствен элемент х₀ÎХ, который принадлежит всем этим шарам т.е. $!х₀Î 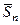(a_n, e_n) "nÎN. ◀ ▶

Полными метрическими пространствами являются множества R и C (вещественных и комплексных чисел) и не является множество Q (рациональных чисел).