Ограниченные множества. Предельные точки

Def: Шаром S(a, r) в метрическом пространстве Х с центром в точке а радиуса r называется множество всех элементов хÎХ удовлетворяющих условию r(a, x) < r : S(a, r) º {xÎX ½r(a, x) < r}.

Def: Множество элементов Х называется ограниченным, если оно целиком принадлежит некоторому шару.

3°. Сходящаяся последовательность ограничена.

◀ Пусть limx_n = х₀. Тогда "e > 0 $N "n > N x_nÎS(x₀, e). Рассмотрим S(х₀, r), где r = max{r(х₁, х₀), r(х₂, х₀), … , r(х_n, х₀), e} + e. Ясно, что "n > N x_nÎS(x₀, r), т.е. последовательность {x_n} ограничена. ▶

Def: Если дано МÌХ, то элемент хÎХ называется предельной точкой или точкой сгущения множества М, если "S(х, e) $х₁ÎМ, х₁ ≠ х такой, что х₁ÎS(х, e).

Def: Множество М с присоединенными к нему всеми предельными точками называется замыканием множества М и обозначается .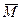

Def: Множество М называется замкнутым, если М = .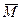

Рассмотрим предельные точки шара S(a, r) и покажем, что все они удовлетворяют требованию r(a, x) £ r. Допустим, что х¢ предельная и r(a, x¢) > r. Тогда в окрестности точки х¢ радиуса 0,5[r(a, x¢) – r] нет ни одной точки шара S(a, r) т.е. х¢ не предельная. Множество 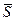(a, r) º {xÎX ½r(a, x) £ r} называется замкнутым шаром.