Предел последовательности

Вектор х₀ метрического пространства Х называется пределом последовательности {х_n} элементов х₁, х₂, … из Х, если последовательность расстояний r(х₀, х₁), r(х₀, х₂), r(х₀, х₃), … , r(х₀, х_n), … стремится к нулю. При этом пишут х_n → х₀ при n → ∞ или limx_n = x₀. Последовательность 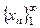, при этом называется сходящейся в Х, или просто сходящейся. Заметим, что 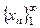, может быть сходящейся и не сходящейся в зависимости от того, в какой метрике рассматривается сходимость.

Например, если есть последовательность 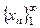, из разных элементов, которая сходится в некоторой метрике r_1, то, введя метрику r_2, (определяемую формулой (*) из §1 мы увидим, что эта последовательность в метрике r_2, не сходится.

1°. Если последовательность 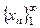, сходится в Х, то сходится и имеет тот же предел, любая подпоследовательность 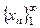, этой последовательности. ◀ ▶

2°. Если последовательность 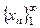, имеет предел то этот предел единственный.

◀ Пусть {х_n} имеет два предела у₁ и у₂. Тогда

"e>0 $N₁ "n > N₁ ½ r(х_n, y₁) < e/2

"e>0 $N₂ "n > N₂ ½ r(х_n, y₂) < e/2.

Выбрав N = max(N₁, N₂) получим

"n > N r(y₁, y₂) £ r(y₁, x_n) + r(х_n, y₂) < e/2 + e/2 = e,

т. е. r(y₁, y₂) < e В силу произвольности e r(y₁, y₂) = 0 т. е. у₁ = у₂. ▶