Ортогональное дополнение к подпространству
Вектор h называется перпендикулярным к подпространству L, если "yÎL, (h, y) = 0.
Если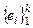 
базис в L (в подпространстве), то (h, ei) = 0, "i = 1, 2, …, k.
Множество векторов hÎL перпендикулярных к подпространству L называется ортогональным дополнением к L и обозначается L^.
7°. L^ является подпространством.
◀ x, yÎL^, zÎL, то (ax + by, z) = a(x, z) + b(y, x) = a×0 + b×0 = 0, т.е. линейная комбинация элементов L^ остается в L^. ▶
8°. V = L ⊕L^.
◀ Пусть {e1, e2, …, ek} базис в L. Дополним его до ортогонального базиса V. {e1, e2, …, ek, fk+1, fk+2, …, fn}. Без ограничения общности можно считать его ортонормированным: 
, где yÎL, zÎL^ и это разложение единственно. ▶
9°. L∩L^ = q.
◀ xÎL, xÎL^ Þ (x, x) = 0 Þ x = q.▶
10°. dimL + dimL^ = dimV. Доказать самостоятельно.
Дата добавления: 2015-05-05; просмотров: 686;