Длина вектора

а) Неравенство Коши-Буняковского |(x, y)|² £ (x, x)×(y, y)

◀ (ax – y, ax – y) = a 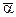(x, х) – a(x, у) – 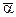(у, х) + (у, у) ³ 0. Пусть 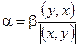, где bÎR. ,

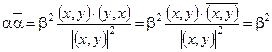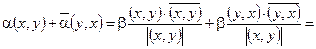
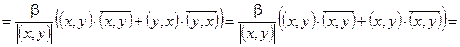
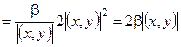. Тогда: (ax– y, ax – y) = b²|x|²– 2b|(x, y)| + |y|²³ 0.

Квадратный трехчлен относительно b сохраняет знак и следовательно:

D £ 0 Þ |(x, y)|² £ |x|²×|y|². ▶

Длиной вектора х в унитарном пространстве V называется величина .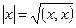

В унитарном пространстве нет содержательного понятия угла, однако, есть понятие ортогональности векторов и понятий с ним связанных, т.к. скалярное произведение является величиной, вообще говоря, комплекснозначной.