Изоморфизм евклидовых пространств
Два евклидовых пространства V и V¢ называются изоморфными, если они изоморфны как линейные пространства и, кроме того, "x, yÎV и "x¢, y¢ÎV¢ (x, y) = (x¢, y¢).
6°. Два евклидовых пространства изоморфны тогда и только тогда, когда dimV = dimV¢.
◀ Необходимость. Пространства изоморфны как линейные и, следовательно,
dimV = dimV¢.
Достаточность. dimV = dimV¢. Пусть 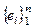 и
и 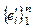 ортонормированные базисы в V и V¢ .
ортонормированные базисы в V и V¢ . 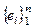 «
« 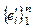 "i = 1, 2, …, n,
"i = 1, 2, …, n, 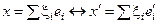 ,
,  ,
,  . ▶
. ▶
Дата добавления: 2015-05-05; просмотров: 992;
