Определение метрического пространства
Пусть в некотором множестве М любой паре его элементов ("х, yÎМ) поставлено в соответствии неотрицательное вещественное число r(х, у), удовлетворяющее следующим аксиомам:
А) r(х, у) = r(х,у) аксиома симметрии;
В) r(х, у) ³ 0, причем r(х, у) = 0 Û х = у аксиома положительности;
С) r(х, у) £ r(х, z) + r(z, у) неравенство треугольника.
В этом случае говорят, что на множестве М задана метрика, функция r(х, у) называется расстоянием, а множество М называется метрическом пространством.
Формально любое множество элементов, в котором определено отношение равенства, можно рассматривать как метрическое пространство, если ввести расстояние так:
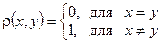 . (*)
. (*)
Дата добавления: 2015-05-05; просмотров: 820;
