И сходимости по норме
Конечномерные нормированные линейные пространства примечательны тем, что в этих пространствах понятие сходимости по норме и координатной сходимости эквивалентны.
10°. Если {хm} сходится покоординатно, то она сходится и по норме.
◀ Пусть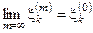 
Þ ║хm – х0║ = 
. ▶
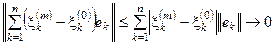11°. Если в конечномерном нормированном пространстве последовательность векторов ограничена по норме, то ограничены и числовые последовательности всех координат в разложении векторов по любому базису. ◀ ▶
12°. В конечномерном нормированном пространстве из сходимости по норме следует координатная сходимость. ◀ ▶
Дата добавления: 2015-05-05; просмотров: 958;