Полилинейный функционал
Если "x1, x2, …, xkÎVn $j(x1, x2, …, xk)ÎK и j(x1, x2, …, xk) линеен по каждому из аргументов x1, x2, …, xk (k £ dimVn) то говорят, что на Vn задан полилинейный (k – линейный) функционал или полилинейная (k – линейная) форма.
Полилинейный функционал называется симметричным по паре аргументов xi и xj , если j(…xi, … xj, …) = j(…xj, … xi, …) и антисимметричным по паре аргументов xi и xj , если j(…xi, … xj, …) = –j(…xj, … xi,…).
Полилинейный функционал называется абсолютно симметричным, если он симметричен по любой паре своих аргументов и антисимметричным, если он антисимметричен по любой паре своих аргументов.
Рассмотрим j(x1, x2, …, xk). x1, x2, …, xkÎVn.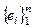 
– базис в Vn. Тогда "i = 1, 2, …, k
xi =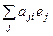 
Þ j(x1, x2, …, xk) =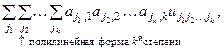 
где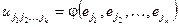 
.
Конструкцию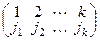 
назовем перестановкой элементов 1, 2, …, k. Обозначим
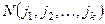– количество беспорядков в перестановке. Беспорядок это когда большее je стоит раньше меньшего jm.
Например, в перестановке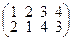 
два беспорядка и N(2, 1, 4, 3) = 2, а в перестановке 
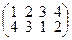пять беспорядков N(4, 3, 1, 2) = 5.
Если функционал j(x1, x2, …, xk) абсолютно антисимметричен, то
j(x1, x2, …, xk) =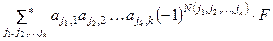 
,
где F = j(e1, e2, …, ek). При этом * у знака S означает, что суммирование идет по всем наборам j1, j2,…, jk и j1, j2,…, jk все разные.
Дата добавления: 2015-05-05; просмотров: 846;