Теорема Лапласа
Пусть задана квадратная матрица Ann. Выберем в матрице A k-строк i1, i2, …, ik и k-столбцов j1, j2, ... jk. Определитель матрицы образованной элементами, стоящими на пересечении выбранных столбцов и строк называется минором kго порядка и обозначается 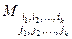 . Если из матрицы А вычеркнуть выбранные строки и столбцы то определитель оставшейся матрицы называется минором дополнительным к минору
. Если из матрицы А вычеркнуть выбранные строки и столбцы то определитель оставшейся матрицы называется минором дополнительным к минору 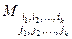 и обозначается
и обозначается 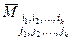 .
.
Величина 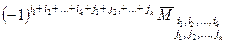 называется алгебраическим дополнением к минору
называется алгебраическим дополнением к минору 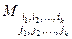 и обозначается
и обозначается 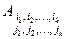 .
.
18°. Теорема Лапласа.
detA = 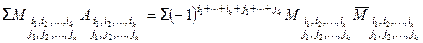 .
.
Суммирование здесь производится по всем минорам kго порядка, стоящим в выбранных k-строках или в выбранных k–столбцах. ◀ ▶
Пример. Вычислить следующий определитель раскрывая его по минорам второго порядка, стоящим во второй и третьей строках определителя:
Существует шесть различных миноров второго порядка, стоящих в указанных строках:
M12= 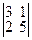
 ; M13=
; M13= 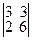 ; M14=
; M14= 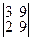 ; M23=
; M23= 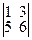 ; M24=
; M24= 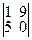 ; M34=
; M34= 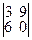 .
.
Дополнительные к ним миноры:

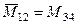 ;
; 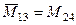 ;
; 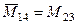 ;
; 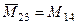 ;
; 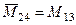 ;
; 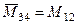 .
.
Найдем соответствующие алгебраические дополнения:
A12 = (-1)2+3+3+4 M34 = M34; A13 = (-1)2+3+2+4 M24 = -M24; A14 = (-1)2+3+2+3 M23 = M23; A23 = (-1)2+3+1+4 M14 = M14; A24 = (-1)2+3+1+3 M13 = -M13; A34 = (-1)2+3+1+2 M12 = M12.
Теперь, используя теорему Лапласа, можно записать:
D = M12A12 + M13A13 + M14A14 + M23A23 + M24A24 + M34A34 = M12M34 - M13M24 + M14M23 + + M23M14 - M24M13 + M34M12 = 2 ( M12M34 - M13M24 + M14M23 ) = 2 (-13×54+12×45-9×11) = –522.
Дата добавления: 2015-05-05; просмотров: 884;
