Метод представления определителя в виде суммы определителей.
Вычислить определитель:  .
.
Заметив, что элементы первого столбца представлены как суммы двух чисел, разложим определитель в сумму двух определителей:
 .
.
Теперь каждый из полученных определителей разложим в сумму двух определителей, воспользовавшись тем, что элементы вторых столбцов у них также представлены в виде сумм, и т.д. Проделав это, получим (n > 2), что строки полученных определителей будут такими: ai, ai, … , ai или b1,b2,… ,bn . Строки 1го типа пропорциональны, 2го типа равны и, следовательно, все слагаемые равны нулю. Следовательно: Dn = 0 ("n > 2).
Для определителей такого же типа, но первого и второго порядков получим:
D1 = | a1+ b1 | = a1+ b1; D2 = 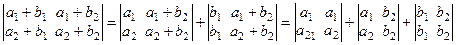 =
=
= a1b2– a2b2+ b1a2 – a1b1 = (a1 – a2)b2 + (a2 + a1)b1 = (a1 – a2)(b2 – b1).
Метод рекуррентных (возвратных) соотношений.
Вычислить определитель n–го порядка:  .
.
Разлагая определитель по элементам первой строки, получим рекурентное соотношение: Dn=  .
.
Разложив определитель в правой части соотношения по первому столбцу, запишем новое рекурентное соотношение: Dn = 5Dn–1 – 6Dn–2.
Представляя это соотношение в виде: Dn – 2Dn–1 = 3(Dn–1 – 2Dn–2) и вводя обозначение:
Тn = Dn – 2Dn–1 получим: Тn = 3Тn–1 – 32Тn–2 = … =3 n-2T2=3n.
Аналогично, записав рекурентное соотношение в виде: Dn – 3Dn–1 = 2(Dn–1 – 3Dn–2) и обозначая: Vn = Dn – 3Dn–1 получим Vn = 2Vn=1 = 22Vn–2=…= 2n .
| |
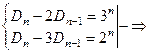 Dn = 3n + 1 – 2n + 1.
Dn = 3n + 1 – 2n + 1.
В общем случае, для рекуррентных соотношений типа: Dn = pDn – 1 + qDn – 2 .можно проделать следующее: пусть a и b корни уравнения x2 – px – q = 0, т.е. p = a + b,
q = –ab. Тогда Dn = aDn – 1 + bDn –1 – abDn – 2; Dn – aDn -–1 = b(Dn – 1 – aDn – 2), т.е. Sn = bSn – 1 или Dn – bDn -–1 = a(Dn – 1 – bDn – 2), т.е. Vn = bVn – 1 .
Аналогично можно поступить и в более сложных рекуррентных соотношениях.
Дата добавления: 2015-05-05; просмотров: 3226;
