Метод выделения линейных множителей.

а) Вычислить определитель .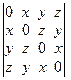

1. Прибавляя к первому столбцу определителя остальные три, обнаружим, что в первом столбце есть общий множитель, который равен х + у + z. Следовательно, определитель делится на х + у + z.

2. Аналогично, прибавляя к первому столбцу второй и вычитая из него третий и четвертый столбцы, получаем, что определитель делится на х – у – z.

3. Если первый столбец сложить с третьим и вычесть второй и четвертый, то получим, что определитель делится на х – у + z.

4. Если к первому столбцу прибавить четвертый и вычесть второй и третий столбцы, то обнаружим, что определитель имеет множитель х – у + z. Итак:

= .

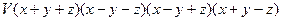Ясно, что определитель является многочленом 4^й степени по x, по y и по z. Справа тоже многочлен той же степени. Поэтому V = const. В определитель x⁴ входит в слагаемом:

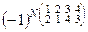a₁₂a₂₁a₃₄a₄₃ = (–1)²×х×х×х×х = х⁴.

В правой части старший член по х: Vx⁴, т.е. V = 1. Получаем результат:

= (x + y + z)(x – y – z)(x – y + z)(x + y – z) = x⁴ + y⁴ + z⁴ – 2x²y² – 2x²z² – 2у²z².

б) Вычислить определитель n-го порядка: .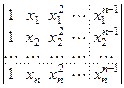

Этот определитель называется определителем Вандермонда. Рассматривая его как многочлен (n –1)^й степени относительно x_n увидим, что он обращается в 0 при x_n = x_1, x_n = x_2, … x_n = x_{n – 1}. Тогда D_n = a_{n – 1}(x_n – x₁)(x_n – x₂) … (x_n – x_n–1), причем a_n–1 = = D_n–1. Повторяя эту процедуру, получим: D_n = (x₂ – x₁)(x₃ – x₂)(x₃ – x₁)(x₄ – x₃)(x₄ – x₂)(x₄ – –x₁)… = .