Унитарные операторы

Def: Линейный оператор UÎL(V, V) называется унитарным, если

"х, yÎV (Ux, Uy) = = (x, y) .

1° Из условия унитарности: ||Ux|| = ||x||, ||U|| = 1.

2° Если λ – собственное значение унитарного оператора, то | λ | =1.

◀ Пусть е – собственный вектор с собственными значениями λ и ||x|| = 1. Тогда

| λ | =| λ | || e|| = ||le|| = ||Ue|| = || e|| =1 ▶

Тº. Чтобы линейный оператор UÎL(V, V) был унитарным необходимо и достаточно,

чтобы U^* = U^–1.

◀ Необходимость: Пусть U – унитарный Þ (Ux, Uy) = (x, y) Þ (x, U^*Uy) = (x, y) Þ

Þ (x, (U^*U - Е)у) = 0 Þ U^*Uy = Еу Þ U^*U = Е Þ U^* = U^-1.

Достаточность: Пусть U^* = U^-1 Þ U^*U = Е Þ (х, у) = (х, U^*Uу) = (Ux, Uy), т.е. U – унитарный ▶

Примечание: U^* = U^-1 Û U^*U = UU^* = Е Û (Ux, Uy) = (x, y).

В примечании приведено две эквивалентные формы записи условия унитарности оператора.

Нетрудно убедиться в том, что произведение унитарных операторов – унитарный оператор.

Def: Оператор l называется унитарно подобным оператору L, если существует унитарный оператор U такой, что l = U^*LU,

Напомним, что 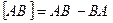– называется коммутатором операторов А и В. При этом, если 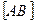= 0, то А и В коммутирующие операторы.

Обозначим j = U^*y.

Для унитарно подобных операторов выполняются следующие соотношения:

1) [L, M] = N Þ [l, m] = n; 2) L = L^* Þ l = l^*;

3) Ly = ly Þ lj = lj; 4) (Ly₁, y₂) Þ (lj₁, j₂).