Полуторалинейные эрмитовы формы

Def: Полуторалинейная форма В(х, у) называется эрмитовой, если "x, yÎV: .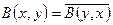

Мы уже отмечали: "В(х, у) – полуторалинейные формы $! А – линейный оператор такой, что В(х, у) = (Ах, у).

Тº. Для того, чтобы полуторалинейная форма В(х, у) была эрмитовой необходимо и

достаточно, чтобы оператор А (В(х, у) = (Ах, у)) был эрмитовым.

◀ Достаточность: Пусть А – эрмитов, т.е. А = А^* Þ В(х, у) = (Ах, у) = (х, Ау) = =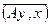

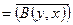, т.е. форма В(х, у) – эрмитова.

Необходимость: Пусть форма эрмитова Þ (Ах, у) = В(х, у) = 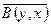= = 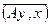(х, Ау), т.е.

А – эрмитов ▶

Тº. Для того, чтобы форма В(х, у) была эрмитовой необходимо и достаточно, чтобы

В(х, х) была вещественной "хÎV.

◀ В(х, у) – эрмитова Û А – эрмитов. А – эрмитов Û А(х, у)ÎR ▶

предыдущая доказано ранее

теорема