Взаимодействие между элементами симметрии в кристалле
В 1867г. А.В. Годолиным было доказано, что количество кристаллографических формул, которыми можно описать любой кристалл, существует в природе ограниченным числом 32 (табл. 3.1). Это доказательство он вывел на основании геометрических законов о взаимодействии элементов симметрии между собой.
Общая теорема: Наличие двух взаимодействующих элементов симметрии обязательно влечет за собой наличие третьего элемента, действие которого равно сумме действий первых двух элементов.
Теорема 1. Линии пересечения двух плоскостей симметрии есть ось симметрии, угол поворота которой в два раза больше угла между плоскостями.
Теорема 2. Пересечение двух осей симметрии 2-го порядка порождает третью ось, перпендикулярную к ним в точке пересечения. Угол поворота этой оси в два раза больше угла между пересекающимися осями.
Теорема 3. Взаимодействие двух элементов симметрии из троих: четной оси, перпендикулярной к ней плоскости и центра симметрии порождает третий, т.е. если имеется два из них, то обязательно будет третий.
Теорема 4. Если имеются ось Ln и перпендикулярно к ней проходит ось L2, то число осей L2 будет n.
Теорема 5. Если имеется ось Ln и параллельно ей проходит плоскость симметрии, то число таких плоскостей будет n. Кроме того, может быть еще одна перпендикулярная к оси плоскость симметрии.
Таблица 3.1 - Распределение 32 классов по сингониям и категориям
| Категория | Сингония | Примитивный | Центральный | Планальный | Аксиальный | Планаксиальный | Инверсионно-примитивный | Инверсионно-планальный |
| Низшая | Триклинная | 1 | 2 C | |||||
| Моноклинная | 3 P | 4 L2 | 5 L2PC | |||||
| Ромбическая | 6 L22P | 7 3L2 | 8 3L23PC | |||||
| Средняя | Тригональная | 9 L3 | 10 L3C | 11 L33P | 12 L33L2 | 13 L33L23PC | ||
| Тетрагональная | 14 L4 | 15 L4PC | 16 L44P | 17 L44L2 | 18 L44L25PC | 19 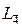
| 20 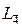 2L2 2P=3L2 2P 2L2 2P=3L2 2P
| |
| Гексагональная | 21 L6 | 22 L6PC | 23 L66P | 24 L66L2 | 25 L66L27PC | 26 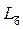 =L3P =L3P
| 27 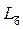 3L23P=L3 3L24P 3L23P=L3 3L24P
| |
| Высшая | Кубическая | 28 4L33L2 | 29 4L33L23PC | 30 4L33L26P | 31 3L44L36L2 | 32 3L44L36L29PC |
Дата добавления: 2015-06-27; просмотров: 2162;
