Элементы симметрии

Симметрия – это закономерное повторение равных фигур или равных частей одной и той же фигуры в пространстве.

Если геометрический объект в трехмерном пространстве повернут, смещен или отражен и при этом он преобразовался сам в себя, то есть остался инвариантен к преложенному преобразованию, то такой объект называется симметричным, а преобразование симметрическим.

Все монокристаллы ограничены в пространстве элементами ограничения – это грани, ребра, вершины и двухгранные углы.

Элементы симметрии кристаллов – закономерное повторение одинаковых элементов ограничения кристалла (вершин, граней, ребер) относительно воображаемых линий, плоскостей, точек (элементов симметрии).

Центр симметрии (C) – точка внутри фигуры, по отношению к которой в диаметрально-противоположных направлениях на равных расстояниях находятся одинаковые элементы фигуры (рис. 3.1) .

Рисунок 3.1 - Центр симметрии

Чтобы найти центр симметрии, надо положить многогранник на стол поочередно каждой гранью и проверить, есть ли вверху грань, расположенная горизонтально; обе грани – верхняя и нижняя должны быть одинаковыми и параллельными. Если даже для одной из граней не соблюдается указанное условие , то центр симметрии отсутствует.

Осью симметрии ( L_n ) называется воображаемая прямая линия, при повороте вокруг которой на определенный угол (a) фигура совмещается сама с собой. Число совмещений при полном обороте (на 360⁰) определяет порядок оси:

n=360^о/a

В кристаллах имеются оси 1, 2, 3, 4 и 6-го порядка, при этом a = 360, 180, 120, 90, 60. Оси первого порядка не учитываются, так как в любом кристалле их бесконечное множество, а осей 5-го порядка и выше 6-го не допускает решетчатость структуры кристаллов.

Основной закон симметрии:

Ln ≠L₅ и L_{( > 6 )}

Примеры осей различного порядка для плоских фигур показаны на рис. 3.2.

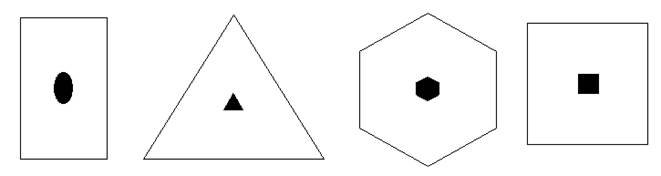
Рисунок 3.2 - Оси симметрии плоских фигур

В кристаллических многогранниках оси симметрии проходят через центр тяжести фигуры, а их выходы на поверхности - совпадают либо с вершинами, либо с серединами ребер (рис. 3.3):

а б в

Рисунок 3.3 - Оси симметрии куба: а) 3L₄ , б) 6L₂, в) 4L₃

Для определения порядка оси симметрии фигуру в точках выхода предполагаемой оси закрепляем пальцами руки. Запоминаем исходное положение всех элементов ограничения. Вращая модель вокруг закрепленной оси, наблюдаем, сколько раз при полном обороте фигура совместится с первоначальным положением: число совмещений, включая начальное, есть порядок оси. Заметим, что пока найдена единственная ось, а чтобы найти все остальные, надо таким же образом проверить попарно все противолежащие вершины, середины граней ребер.

Для фигур, имеющих центр симметрии, оси симметрии проходят:

- через противоположные вершины;

- через центры противоположных граней;

- через середины противоположных ребер.

Для фигур, не имеющих центра симметрии, кроме перечисленных выше случаев, оси симметрии могут проходить:

- по линиям вершина – центр грани;

- по линиям центр ребра – центр грани (рис. 3.4).

Если ось перпендикулярна к грани, то ее порядок соответствует симметрии той фигуры (рис.3.1), в виде которой представлена грань.

Число граней, сходящихся в вершине гранного угла, отвечает порядку оси (рис. 3.3в, 3.4).

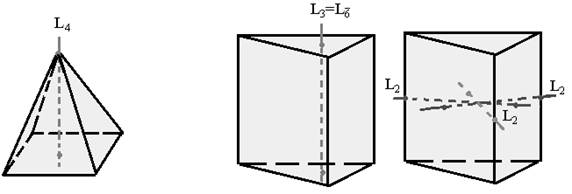
а б

Рисунок 3.4 - Оси симметрии в несимметричных фигурах: а) тетрагональной пирамиде, б) тригональной призме

Практическая рекомендация. Для кристаллов средней категории, если найдена ось симметрии высшего порядка L_3, L_4, L₆, то оси L₂ следует искать в плоскости, перпендикулярной оси симметрии высшего порядка. Кристаллы средней категории можно определить по их форме: такие кристаллы развиты одинаково в двух перпендикулярных направлениях, а в третьем – либо вытянуты, либо сплющены.

Рисунок 3.5 – Построение инверсионной оси

Помимо простых осей симметрии существуют еще и сложные (инверсионные) оси. Инверсионной осью называется линия, при вращении вокруг которой на определенный угол и последовательном отражении фигуры через геометрический центр произойдет совмещение фигуры с исходным положением (рис. 3.5).

Инверсионные оси бывают:

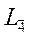- четверная сложная (инверсионная) ось, может совпадать с простой двойной осью симметрии (при отсутствии центра симметрии). При повороте этой фигуры вокруг этой оси на 90^о и последующем ее отражении в центральной точке, фигура совмещается сама с собой. Такая ось наблюдается, например, в тетрагональных тетраэдре и скаленоэдре.

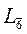- шестерная сложная (инверсионная) ось, всегда совпадает с простой тройной осью симметрии при наличии перпендикулярной к ней плоскости симметрии ( 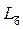= L₃ + P см. рис. 3.4, б).

Плоскость симметрии Р – плоскость, разделяющая фигуру на две зеркально равные части, расположенные относительно друг друга как предмет и его зеркальное изображение (рис. 3.6).

а б в г

Рисунок 3.6 - Плоскости симметрии в равнобедренном треугольнике (а), квадрате (б), прямоугольнике (в), ромбе (г)

Плоскости симметрии могут проходить через середины граней и ребер многогранника, перпендикулярно к ним; или через вершины, по ребрам, образуя равные углы с одинаковыми гранями и ребрами.

Максимальное количество плоскостей 9 Р в кубе: три взаимно перпендикулярные проходят через середины граней и ребер , шесть плоскостей - диагональные (рис. 3.7).

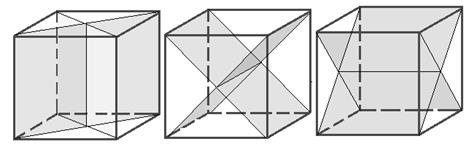
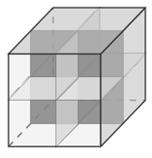
Рисунок 3.7 - Плоскости симметрии в кубе

При определении плоскостей симметрии модель необходимо держать в руках, не переворачивая ее.

Сочетание элементов симметрии для данного многогранника дает нам кристаллографическую формулу симметрии. В формуле на первом месте последовательно записываются оси симметрии (от осей высшего порядка к осям низшего порядка), а затем плоскости и в конце – центр симметрии. Например, формула симметрии куба 3L₄ 4L₃ 6L₂ 9PC .