Распределение простых форм по сингониям и категориям
Простой формой называют совокупность граней, выводящихся друг из друга при помощи элементов симметрии. К одной простой форме относятся те грани, которые имеют одинаковые форму и размер.
Перебрав 32 комбинации кристаллографических формул с учетом теорем взаимодействия, находим, что в природе может существовать всего лишь 47 простых форм.
Названия большинства форм основаны на следующих древнегреческих словах:
| 1 - моно | 5- пента | 12-додека |
| 2 –ди | 6 – гекса | пинакэ - доска |
| 3 – три | 7 – гепта | эдр - грань |
| 4 - тетра | 8 - окта | гон - угол |
Простые формы подразделяются на открытые (не замыкающие полностью пространство) – моноэдр, диэдр, пинакоид, призмы, пирамиды, и закрытые (полностью замыкающие пространство) – дипирамиды, ромбоэдр, трапецоэдры, куб, октаэдр, скаленоэдры, тетраэдры, додекаэдры и др.
Все простые формы распределяются по категориям и сингониям: для кристаллов низшей категории возможны 7 простых форм, средней – 25 и высшей – 15.
 Простые формы низшей категории (рис.4.1) - это:
Простые формы низшей категории (рис.4.1) - это:
1.  Моноэдр – одна грань любой формы (в единственном числе)
Моноэдр – одна грань любой формы (в единственном числе)
2.  Пинакоид – две параллельные грани любой формы.
Пинакоид – две параллельные грани любой формы.
3. Диэдр – две драни, пересекающиеся под углом
4. Ромбическая призма – призма, в сечении которой ромб, грани параллельны главной оси симметрии
5. Пирамида ромбическая
6. Дипирамида ромбическая
7. Тетраэдр ромбический – четыре грани в форме разностороннего треугольника
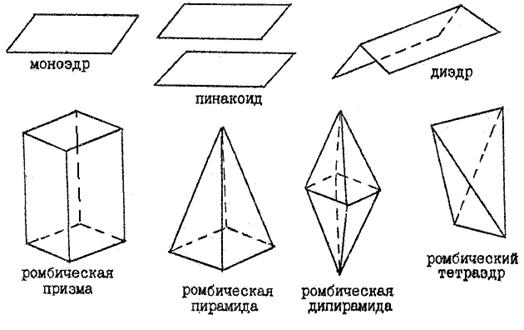
Рисунок 4.1 – Простые формы низшей категории
Простые формы средней категории (табл. 4.1).
К средней категории относится 25 простых форм. Кроме того, в кристаллах средней категории встречаются еще 2 простые формы из низшей категории – моноэдр и пинакоид.
Таблица 4.1 - Простые формы средней категории
| Сингония | Тригональная | Тетрагональная | Гексагональная |
| Главная ось | L3 | L4 ( 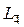 ) )
| L6 ( 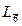 ) )
|
| Характерное поперечное сечение (перпендикулярное главной оси) | 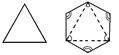 тригон дитригон
тригон дитригон
| 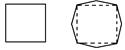 тетрагон дитетрагон
тетрагон дитетрагон
| 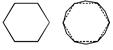 гексагон динексагон
гексагон динексагон
|
| Призмы – грани параллельные главной оси симметрии. Кроме тригональной сингонии, они еще и попарно параллельны | 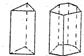 тригональная дитригональная
тригональная дитригональная
| 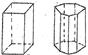 тетрагональная дитетрагональная
тетрагональная дитетрагональная
| 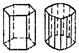 гексагональная дигексагональная
гексагональная дигексагональная
|
| Пирамиды – грани наклонены друг к другу и пересекают главную ось в одной точке | 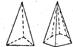 тригональная дитригональная
тригональная дитригональная
| 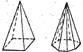 тетрагональная дитетрагональная
тетрагональная дитетрагональная
| 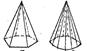 гексагональная дигексагональная
гексагональная дигексагональная
|
| Дипирамиды– пирамиды, сложенные донышками | 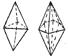 тригональная дитригональная
тригональная дитригональная
| 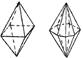 тетрагональная дитетрагональная
тетрагональная дитетрагональная
| 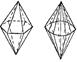 гексагональная дигексагональная
гексагональная дигексагональная
|
| Трапецоэдры | 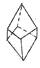 тригональный тригональный
|  тетрагональный тетрагональный
| 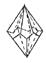 гексагональный гексагональный
|
| Тетраэдр -верхняя грань расположена симметрично относительно двух нижних | - | 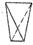 тетрагональный ( тетрагональный ( 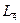 ) )
| - |
| Ромбоэдр– сплюснутый или вытянутый вдоль оси L3 куб, верхняя грань расположена симметрично относительно двух нижних | 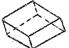
| - | - |
| Скаленоэдры – грани пересекают главную ось в двух точках и нижняя пара граней расположена симметрично относительно двух пар верхних граней | 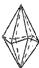 тригональный тригональный
| 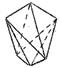 тетрагональный тетрагональный
| - |
Простые формы высшей категории (кубической сингонии) (рис. 4.2).
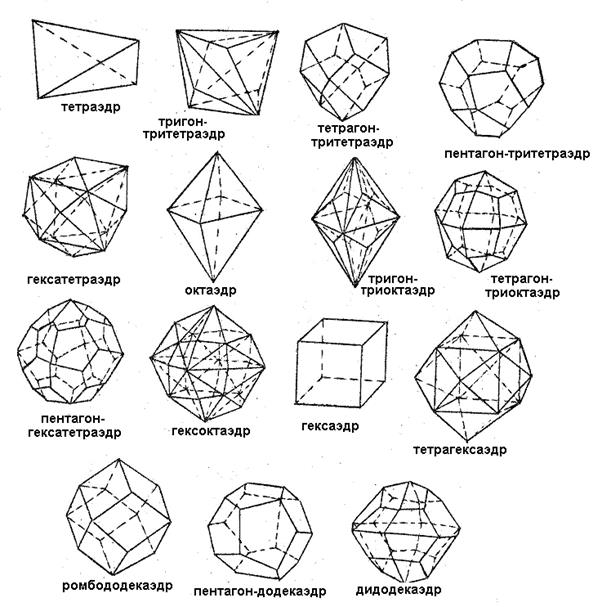
Рисунок 4.2 – Простые формы кубической сингонии
Из них различают исходные формы и производные. К исходным формам относят:
1. тетраэдр кубический (грани - 4 равносторонних треугольника);
2. гексаэдр (куб);
3. октаэдр (грани - 8 равносторонних треугольников);
4. ромбододекаэдр (12 граней в виде ромба);
5. пентагондодекаэдр (12 граней в виде пятиугольника).
Производные формы образуются из исходных путем надстраивания различных пирамид на гранях исходной формы, причем размножение исходной грани может происходить в 2, 3, 4 и 6 раз.
Надстраивание производных форм строятся следующим образом:
Тригонтритетраэдр:
тригон - форма новой грани, образовавшейся на исходной грани,
три – количество новых граней на одной исходной,
тетраэдр – название исходной формы.
Простые формы кубической сингонии легко определяются по количеству граней, относящихся к одному сорту:
- если грани четыре, то это кубический тетраэдр
- если таких граней шесть, то это куб
- если их восемь – октаэдр.
Гексаоктаэдр (48 граней) – максимальное количество граней в природе.
Дата добавления: 2015-06-27; просмотров: 9524;
