Установка кристаллов

Для определения кристаллографических символов и изображения стереографических проекций пользуются стандартными международными правилами установки кристаллов.

Установка кристалла – это выбор кристаллографических осей, единичной (масштабной) грани и его ориентировка в пространстве относительно этих осей и грани.

Кристаллографические системы координат зависят от симметрии кристаллов и изменяются по сингониям. Для кристаллов тригональной и гексагональной сингоний принимаются четыре оси x, y, z, u, а для остальных сингоний x, y, z.

В кристаллографии используется два вида кристаллографических осей: трехкоординатная и четырехкоординатная система (рис. 5.2). Четырехкоординатная система используется в тригональной и гексагональной сингониях, а трехкоординатная – для кристаллов триклинной, моноклинной, ромбической, тетрагональной и кубической сингоний.

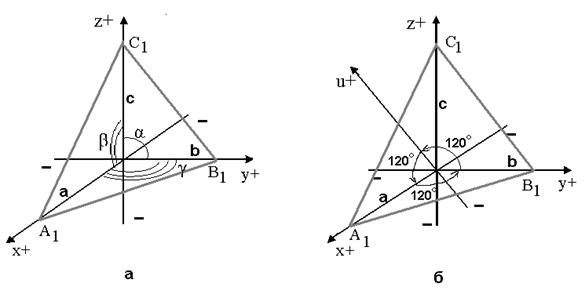
Рисунок 5.2 - Направления кристаллографических осей в: а – трехкоординатной, б – четырехкоординатной системах

Для трехкоординатной принята правая система координат, то есть положительными направлениями считаются: для оси Х – вперед на наблюдателя, У – вправо от наблюдателя, Z – вверх. В четырехкоординатной системе оси x, y, u, лежат в одной плоскости, угол между ними составляет 120°, ось z -перпендикулярна им.

Единичную грань принимают таким образом, чтобы она пересекала либо все координатные оси, либо максимальное их число. При этом масштабные отрезки, отсекаемые ею, принимаются за единицы измерения по соответствующей координатной оси.

Для каждой сингонии характерными являются углы между координатными осями: между x и y –α, между z и x – β, между x и y – γ и масштабные отрезки (единичные параметры) на координатных осях: на оси x отрезок обозначается а, на оси у – в, на оси z – с.

Таблица 5.1 - Характеристика систем координат в зависимости от сингонии

Сингония	Выбор координатных осей	Координатные углы и единичные параметры	Единичная грань
Триклинная	За оси x,y,z принимают три ребра, которые пересекались бы под углами, более близкими к 90°. За вертикальную ось брать ребро наиболее развитой зоны.	α≠β≠γ≠90° а≠в≠с	Грани пинакоида или моноэдра
Моноклинная	Ось y – L2или ׀ Р, x, и, z – два ребра, перпендикулярные оси У; x- вперед наклонно вниз, z – вертикально вдоль ребра наиболее развитой зоны	α= γ=90°≠β β≠120° а≠в≠с	Грани ромбической призмы или диэдра
Ромбическая	х, у -2L2или нормали к 2Р, Z-L2	α=β=γ=90° а≠в≠с	Грани дипирамиды или тетраэдра
Тетрагональная	Z-L4( 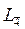), x,y-2L2или нормали к 2Р(под углом 90°), при отсутствии – два ребра под углом 90°	α=β=γ=90° а=в≠с	Грани пирамиды или тетраэдра или дипирамиды
Кубическая	x,y,z - 3L4 при отсутствии 3L2	α=β=γ=90° а=в=с	Грани октаэдра или тетраэдра
Тригональная или Гексагональная	Z- L3, L6( 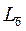), x,y,u -2L2 или их отсутствии – три перпендикулярные к оси z ребра под углами 60°	α=β=90° а=в≠с γ=120°	Грани пирамиды, дипирамиды, ромбоэдра

Оси координат располагаются в соответствии с симметрией кристаллов либо по осям симметрии, либо по нормалям к плоскостям, а если их нет – по ребрам кристаллического многогранника. В табл. 5.1 приведены правила установки кристаллов по сингониям, а также характеристики координатных систем. Фактически в каждой сингонии своя система координат, которая отличается от системы координат другой сингонии координатными углами и единичными параметрами. Только в тригональной и гексагональной сингониях используется единая четырехкоординатная система.

5.3 Закон Гаюи

Открыл этот закон в 1784 году Жан Огюст Гаюи. Это учение о символах основывается на одном из важнейших законов кристаллографии – законе рациональности отношений параметров (закон Гаюи).

Предположим, что тщательно изучив наши рекомендации по установке кристаллов, вы правильно расположили модель кристалла в координатной системе, приняв за координатные оси три непараллельных ребра. А теперь пронаблюдайте, где пересекают координатные оси две грани Вашего кристалла при их мысленном продолжении (рис. 5.3). Одна – единичная, А₁,В₁,С₁, выбранная в соответствии с сингонией по правилам табл. 5.1, отсекает отрезки ОА₁, ОВ₁, ОС₁, называемые единичными параметрами. Другая непараллельная грань (A_x, B_x, C_x) характеризуется параметрами ОA_x, ОB_x, ОC_x.

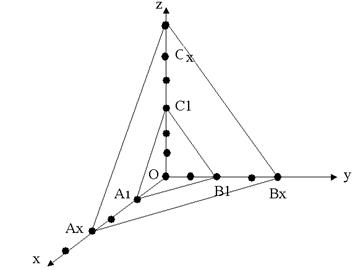
Рисунок 5.3 - Параметры и кристаллографические оси

Закон Гаюи гласит: двойные отношения параметров, отсекаемые двумя любыми гранями кристалла на трех пересекающихся ребрах его, равны отношениям целых и сравнительно малых чисел

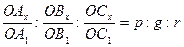(параметры Вейса)

Наличие целых чисел объясняется решетчатым строением кристаллов. Ребра кристалла соответствуют рядам решетки, грани – плоским сеткам. Плоские сетки - (грани), пересекая три ряда решетки (ребра), образуют на них отрезки (параметры), содержащие целые числа промежутков между узлами решетки (элементарными частицами) (рис. 5.3).

Наличие малых чисел связано с тем, что реальные грани кристаллов построены не любыми плоскими сетками, а только теми, которые обладают наибольшей плотностью расположения в них элементарных частиц.

Закон Гаюи связывает внешнюю форму кристаллов с их внутренним решетчатым строением.

При практическом применении закона Гаюи для определения индексов граней пользуются обратными отношениями параметров, получивших название индексов Миллера:

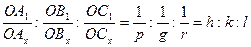
Индексы Миллера – это величины, обратные параметрам Вейса, приведенные к целым числам. Для получения индексов Миллера в виде трех взаимно простых чисел проводят следующие математические преобразования:

- приводят дроби к общему знаменателю,

- находят дополнительный множитель,

- отбрасывают общий знаменатель,

- сокращают полученное соотношение на общий множитель.

Для примера определим индексы Миллера грани А_xВ_xС_x (рис. 5.3), параметры выразим числом промежутков между элементарными частицами (или в мм, см):

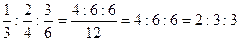
Индекс грани А_xВ_xС_x - (2 3 3).

Таким образом, любую грань (А_xВ_xС_x), а точнее - ее наклон к кристаллографическим осям, можно охарактеризовать тремя целыми и взаимно простыми числами – индексами ( 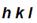), представляющими отношения трех дробей, числители которых являются параметрами единичной грани (ОА₁,ОВ₁, ОС₁), а знаменатели соответствуют параметрам искомой грани (А_x, В_x, С_x). После математических преобразований индексы имеют вид небольших целых чисел. Чем больше параметр грани, то есть, чем больший отрезок отсекает грань на координатной оси, тем меньший индекс она имеет по данной оси.

Условное обозначение символов:

Грань – ( 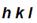) или ( 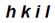) – для кристаллов тригональной и гексагональной сингоний, h – индекс по оси X, k – индекс по оси Y, і – индекс по оси U , l – индекс по оси Z; простая форма – { 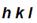}; ребро – [ 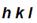] (ряд кристаллической решетки) ; вершина – [[ 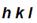]] (узел кристаллической решетки).

Если грань пересекает какую-то ось с отрицательной стороны, то над индексом по этой оси ставят знак минус ( ).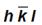

В качестве символа простой формы выбирается грань, обладающая максимальным количеством положительных индексов.

На практических занятиях по кристаллографии отрезки, отсекаемые гранями на координатных осях определяем приблизительно при помощи линейки и карандаша. Более точные вычисления производятся на основании специальных формул с применением гониометрических измерений.

5.4 Практические рекомендации по определению кристаллографических символов

Практические рекомендации по определению кристаллографических символов заключаются в следующем:

1. Символ единичной грани, если она пересекает все три координатные оси, (111), независимо от того, какие отрезки – равные или неравные отсекает она по этим осям. В этом легко убедится, подставив в общую формулу вместо ОА_x , ОВ_x, ОС_x ее параметры ОА₁,ОВ₁, ОС₁.

Доказательство:

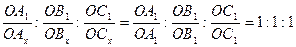
Символ грани А_xВ_xС_x (111)

2. Если грань, в том числе единичная, параллельна одной или двум координатным осям, то индекс, соответствующий данным осям, равен нулю. Пусть грань параллельна оси x и y, т. е.

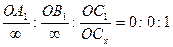
Символ грани (001)

3. Для определения символа грани кристалла кубической сингонии достаточно измерить ее отрезки, которые отсекает эта грань по координатным осям, и взять величины им обратные, т.к. ОА₁=ОВ₁= ОС₁.Тогда

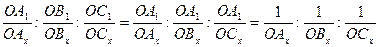
Индексы некоторых простых форм кубической сингонии:

гексаэдр{100}, октаэдр{111}, тетраэдр{111}, ромбододекаэдр {110}, пентагондодекаэдр {hk0}, тетрагексаэдр {hk0}, гексаоктаэдр {hkl}

4. В тетрагональной сингонии ОА₁= ОВ₁≠ ОС₁, поэтому общая формула 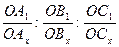принимает вид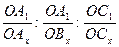

В случае вертикальных граней, т.е. при ОС_x= ∞

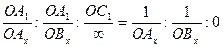
Индексы некоторых простых форм тетрагональной сингонии:

пинакоид {001}, моноэдр {001}{001}, тетрагональные призмы {100},{110},{hk0}, тетрагональные пирамиды и дипирамиды {111}, {101}, {h0l}, {hhl}, {hkl}.

5. В триклинной, моноклинной и ромбической сингониях часто реальная единичная грань, пресекающая все три координатные оси, отсутствует. В указанных сингониях чаще всего используются индексы .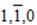

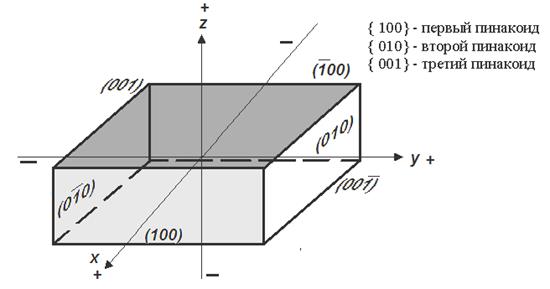
Рисунок 5.4 - Символы граней и простых форм прямоугольного параллелепипеда (ромбическая сингония)

Индексы некоторых простых форм низшей категории:

Ромбические призмы и диэдры {110}, {101}, {011}, {h0l}, {0kl}, ромбические пирамиды и дипирамиды {111}, {hkl}.

6. За единичную грань в тригональных и гексагональных кристаллах принимают такую грань, которая отсекает равные отрезки на двух горизонтальных осях, и неравный - по оси Z.

Возможны два случая установки:

1) Грань, отсекающая равные отрезки на двух соседних осях, образующих друг с другом угол 60°, проходит параллельно третьей (рис.5.5а).

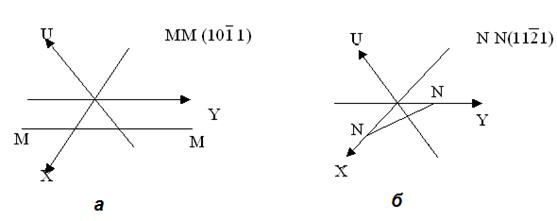
Рисунок 5.5 – Варианты установки кристаллов тригональных и гексагональных сингоний

2) Грань, отсекающая равные отрезки на двух горизонтальных осях, образующих угол 120° и пересекает третью ось (рис. 5.5б). Отрезок по последней оси вдвое короче отрезков по двум другим осям.

Важно заметить, что алгебраическая сумма первых трех индексов всегда равна нулю. Из четырех индексов грани 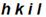третий і не является независимым и определяется первым двумя і = - (h+ k).

Для примера обозначения граней кристаллов с помощью символов вернемся к рис.5.1. Согласно правилу установки (табл.5.1), ось z выбираем вдоль L₄. оси x, y в случае а) – по осям L₂,проходящим через середины ребер кристалла; в случае б) – по осям L₂, проходящим через середины граней. Тогда единичная грань дипирамиды и в том, и в другом случае отсекает на двух горизонтальных осях равные масштабные отрезки и неравный отрезок по третьей оси.

1.Установка кристалла в случае (а)

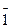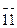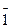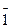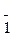
Дипирамида: индексы граней - (111),( 11),( 1),(1 1),(1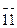1 ),( ),(1 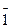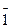),( )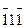; обобщенный символ простой формы {111}.

Призма: индексы граней (110), ( 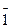10), ( 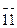0), (1 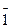0); обобщенный символ простой формы{110}.

2. Установка кристалла в случае (б)

Дипирамида: Индексы граней и символ простой формы аналогично (а).

Призма: индексы граней (100), (010), ( 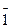00), (0 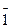0); обобщенный символ простой формы призмы{100}.

Приведенные символы дают ясное представление о неодинаковом расположении граней на обоих кристаллах.