Решетки Браве

В кристаллическом веществе частицы, его слагающие (атомы, ионы, молекулы) расположены в пространстве закономерно, периодически повторяясь. Частицы располагаются по узлам кристаллической решетки. Элементы решетки – ряды, плоские сетки и узлы.

В 1848г. кристаллограф Огюст Браве доказал, что из любой кристаллической решетки можно выделить так называемую элементарную ячейку (параллелепипед повторяемости; решетка Браве).

Всю кристаллическую решетку можно получить путем трансляции (переноса) параллелепипеда повторяемости в пространстве.

Принципы выбора элементарной ячейки:

1) Симметрия ячейки должна отвечать максимально возможному числу элементов симметрии ячейки этого вещества.

2) Элементарная ячейка должна содержать максимальное число прямых углов, или равных углов и равных ребер.

3) Объем ячейки должен быть минимальным.

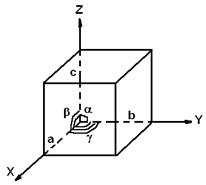
	Параметры элементарной ячейки: a, b, c – ребра α, β, g - углы
Рисунок 7.1 – Элементарная ячейка

Форма ячейки изменяется в зависимости от соотношения параметров. Кроме того, вид ячейки изменяется в зависимости от расположения атомов в этих элементарных ячейках.

Различают следующие виды решеток Браве:

І. Примитивные (Р) – такиеячейки, в которых атомы расположены только по вершинам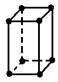
ІІ. Сложные - Базоцентрированные (С) – кроме атомов по вершинам, такие ячейки содержат 2 дополнительных атома по двум базисным граням.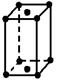
- Гранецентрированные (F) - кроме атомов по вершинам, такие ячейки содержат дополнительные атомы в центре каждой грани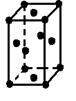
- Объемоцентрированные (J) – кроме атомов по вершинам содержат дополнительный атом внутри в центре элементарной ячейки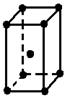

Таблица 7.1 – Зависимость формы ячеек от сингоний

Сингония и примеры	Принцип изменения	Тип решетки Браве
Р	С	F	J
Триклинная K2Gr2O7	Форма ячейки - косоугольный параллелепипед (или комбинация трех пинакоидов). a≠b≠c Ðα≠Ðβ≠Ðg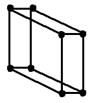
Моноклинная Sb	Сочетание трех пинакоидов a≠b≠c Ðα=Ðβ=90о≠ Ðg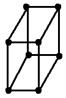
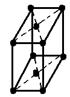
Ромбическая Sa	Сочетание трех пинакоидов в виде «кирпичика» a≠b≠c Ðα=Ðβ=Ðg=90o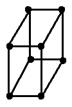
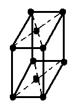
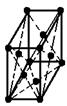
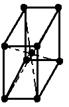
Тригональная (ромбоэдри-ческая) As, Bi	Форма элементарной ячейки – ромбоэдр. Координатные ребра ромбоэдра образуют одинаковые косые углы с главной осью симметрии L3 a=b=c Ðα=Ðβ=Ðg≠90о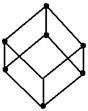
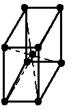
Тетрагональная Snb, TiO2	Форма ячейки – сочетание тетрагональной призмы и пинакоида a=b≠c Ðα=Ðβ=Ðg=90o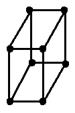
Гексагональная Zn, Cd	В качестве примитивной ячейки принимается ромбическая призма, длинное ребро которой параллельно оси L6, а угол в основании составляет 120о** a=b≠c Ðα=Ðβ=90о, Ðg=120o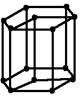
Кубическая Cu, Fe, NaCl	Форма ячейки – куб a=b=c Ðα=Ðβ=Ðg=90o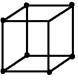

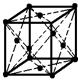
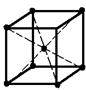
** В связи с тем, что такая элементарная ячейка не соответствует симметрии кристалла, гексагональную решетку можно описать в виде трех ромбических призмочек, соединенных в гексагональную призму. И такая ячейка превращается в базоцентрированную.

Итак, все возможные варианты простых решеток, состоящих из атомов одного типа, можно описать одной из 14-ти решеток Браве. В случае сложных структур описывают решетки по разным типам атомов, а сложную решетку представляют в виде 2-х или 3-х взаимопроникающих простых решеток.

Например, решетку галита (NaCl) описывают как две гранецентрированные кубические решетки, одна из которых по ионам Na⁺, другая – по ионам Cl^-, встроенные друг в друга и сдвинутые на ½ пространственной диагонали куба.

Более детальная классификация структур производится по 230 группам симметрии Федорова. В этих группах кроме уже известных элементов симметрии (осей, плоскостей, центров) добавляются элементы симметрии самой решетки (это – плоскости скользящего отражения, винтовые оси симметрии, трансляция).