АНТЕННЫЕ РЕШЕТКИ С ОПТИМАЛЬНОЙ ДИАГРАММОЙ НАПРАВЛЕННОСТИ

4.1. Условия оптимальности диаграммы направленности

Оптимальными диаграммами принято называть ди­аграммы, наилучшим образом удовлетворяющие различ­ным практическим требованиям. В частности, к антеннам с оптимальной диаграммой направленности относятся ан­тенны, диаграммы нanравленности которых имеют наи­меньший уровень боковых лепестков при заданной ши­рине главного максимума и, наоборот, наименьшую ши­рину главного максимума при заданном уровне боковых лепестков.

Такие антенны называются дольф - чебышевскими оптимальными антеннами. Это название они получили по той причине, что впервые задачу синтеза оптимальной антенны решил Дольф [Л1], используя математический аппарат полиномов Чебышева.

В настоящем пособии и рассматривается методика проектирования дольф — чебышевских антенных реше­ток.

Задача ставится так: спроектировать антенну, диа­грамма направленности которой имеет наименьшую ши­рину главного лепестка при заданном уровне боковых лепестков, или наименьший уровень боковых лепестков при заданной ширине главного максимума. В обоих слу­чаях размеры антенны считаются заданными или выби­раются вначале до решения основной задачи — нахожде­ния токов в излучателях. Оптимальные антенны позво­ляют получить высокую- направленность при низком, на­перед заданном уровне боковых лепестков. Соответствен­но областью применения таких антенн являются системы, в которых предъявляются жесткие требования к уровню бокового излучения. Как правило, это приемные антенны. Примером может служить антенна системы, работающей в условиях большого уровня помех, отстройка от которых производится пространственной селекцией.

Антенна с оптимальной диаграммой направленности представляет собой линейную или двумерную решетку излучателей, размещенных на одинаковом расстоянии друг от друга со специальным амплитудным распределе­нием тока вдоль антенны. Если все излучатели возбуж­даются в фазе, то луч направлен по нормали к антенне. Если задать постоянный сдвиг фаз между излучателями, то луч можно отклонить на необходимый угол.

Для того чтобы диаграмма направленности антенны обладала указанными оптимальными свойствами, необ­ходимо чтобы она описывалась полиномом Чебышева.

Остановимся кратко на свойствах полиномов Чебыше­ва. Это полезно, так как математический аппарат поли­номов Чебышева широко применяется на практике не только при расчете оптимальных диаграмм антенн, но и в теории фильтров, широкополосных согласующих транс­форматоров, направленных ответвителей и ряда других СВЧ устройств.

4.2. Свойства полиномов Чебышева

Полиномами Чебышева называются полиномы вида

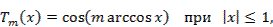
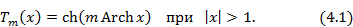
Здесь x — аргумент полинома; m — порядок полинома, определяемый наивысшей степенью переменной х.

Заменив косинус кратного аргумента степенным ря­дом, получим формулы для полиномов Чебышева в виде многочленов.

При m=2N — четном

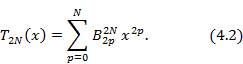
При m = 2N-1 — нечетном

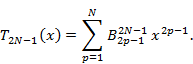
В формулах (4.2) коэффициенты 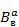— коэффициенты по­линома Чебышева порядка а при в степени переменной х. Эти коэффициенты вычисляются по формулам

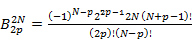, (4.3)

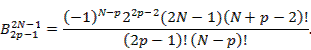
Первые 12 полиномов Чебышева записываются формулами

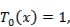
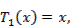
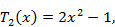
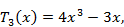
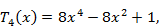
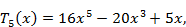
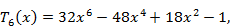
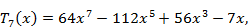
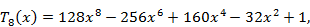
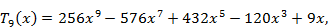
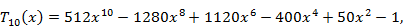
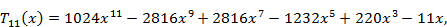
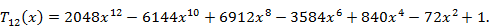
Полиномы Чебышева разных порядков связаны рекур­рентным соотношением

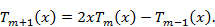
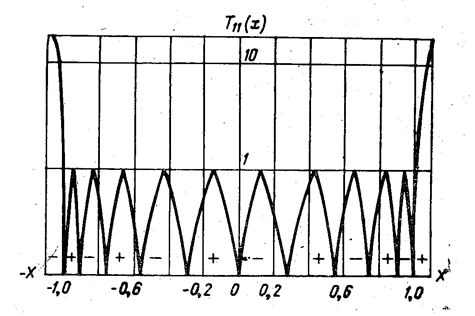
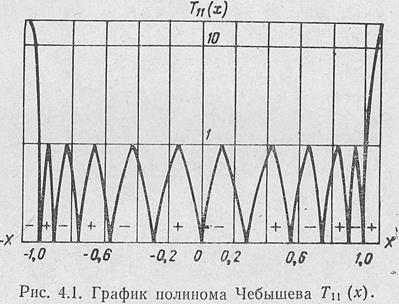
На рис. 4.1 приведен график полинома Чебышева 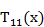. Из приведенного рисунка видно, что полином Че­бышева в пределах изменения аргумента 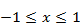пред­ставляет собой знакопеременную функцию с нескольки­ми максимумами. Все максимумы одинаковы и по моду­лю равны единице. За пределами |х| > 1 полином по мо­дулю неограниченно возрастает.

Полином Чебышева обладает следующими свойства­ми, которые и обусловили его широкое применение при построении различных систем.

Из всех степенных полиномов той же степени с дей­ствительными коэффициентами и коэффициентом ори высшем члене, равном :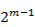

а) в пределах изменения аргумента 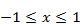поли­ном Чебышева наименее уклоняется от нуля, т. е. абсо­лютные значения максимумов будут наименьшими;

Рис. 4.1. График полинома Чебышева Т11(х).

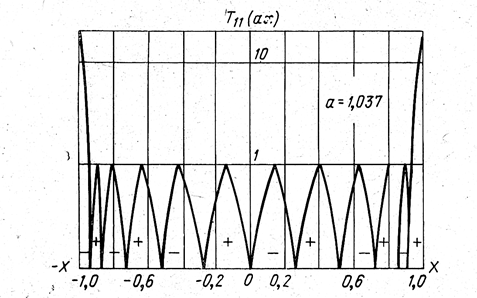
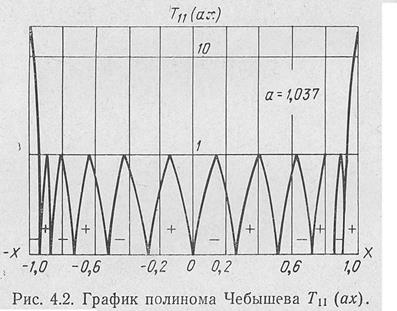
Рис. 4.2. График полинома Чебышева Т11(aх).

б) полином Чебышева имеет наибольшее значение наибольшего корня, т. е. интервал от наибольшего корня до х=1 будет наименьшим. При |х|>1 полином возра­стает, причем скорость нарастания наибольшая.

Теперь рассмотрим те же полиномы, с теми же пре­делами изменения аргумента 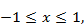но с несколько

измененным масштабом 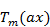, где a>1. На рис. 4.2 изображен тот же полином, что и на рис. 4.1, но при а = 1,037. Как следует из рисунка, график полинома Чебышева теперь приобрел вид диаграммы направленно­сти с главным максимумом и серией боковых лепестков. Уровень боковых лепестков равен 1, а значение функции в максимуме равно 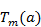. Свойства полинома остались прежними. Он имеет наименьшее значение модуля ле­пестков по отношению к максимуму при x=±1 и наи­большее значение наибольшего корня (наименьшую ве­личину Δx). Отсюда следует, что для того чтобы диа­грамма направленности являлась оптимальной, она должна описываться полиномом Чебышева.

Положение нулей функции 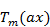определяется со­отношением

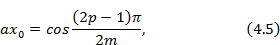
а положение максимумов — формулой

где p=1, 2, 3,... порядковый номер нуля или максимума.

4.3. Диаграмма направленности, описываемая полиномом Чебышева

Антенна с оптимальной диаграммой направленности представляет собой решетку излучателей, размещенных на постоянном расстоянии друг от друга. На рис. 4.3,а

Рис. 4.3. Расположение и нумерация излучателей в решетке: а — число излучателей 2N; б — число излучателей 2N+1.

изображена схема линейной антенны с четным числом излучателей 2N, на рис. 4.3,б — с нечетным числом 2N+1. На рисунке показано расположение излучателей, их нумерация и система координат.

Из всех степенных полиномов той же степени с действительными коэффициентами и коэффициентом при высшем члене, равном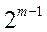

а) в пределах изменения аргумента 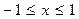поли­ном Чебышева наименее уклоняется от нуля, т. е. абсо­лютные значения максимумов будут наименьшими

б) полином Чебышева имеет наибольшее значение наибольшего корня, т. е. интервал от наибольшего корня до х= 1 будет наименьшим. При | х | >|1полином возра­стает, причем скорость нарастания наибольшая.Теперь рассмотрим те же полиномы, с теми же пре­делами изменения аргумента 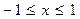- но с несколько

измененным масштабом Т_т(ах), где а>1. На рис. 4.2 изображён тот же полином, что и на рис. 4.но при а = 1,037. Как следует из рисунка, график полинома Чебышева теперь приобрел вид диаграммы направленно­сти с главным максимумом и серией боковых лепестков. Уровень боковых лепестков равен 1, а значение функции в максимуме равно Т_т(а). Свойства полинома остались прежними. Он имеет наименьшее значение модуля ле­пестков по отношению к максимуму при 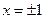и наи­большее значение наибольшего корня (наименьшую ве­личину 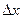): Отсюда следует, что для того чтобы диа­грамма направленности являлась оптимальной, она должна описываться полиномом Чебышева.

Положение нулей функции Т_т(ах) определяется со­отношением

где Р=1, 2, 3,... порядковый номер нуля или максимума