Диаграмма направленности, описываемая полиномом Чебышева
Антенна с оптимальной диаграммой направленности представляет собой решетку излучателей, размещенных на постоянном расстоянии друг от друга. На рис. 4.3,а

изображена схема линейной антенны с четным числом излучателей 2N, на рис. 4.3,6 — с нечетным числом 2N+1. На рисунке показано расположение излучателей, их нумерация и система координат.
Если все излучатели питаются синфазно, то луч на правлен по нормали к линии расположения излучателей ( 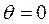 ). Как обычно, диаграмма направленности сложной антенны определяется произведением двух множителей: диаграммы одного элемента на множитель решетки
). Как обычно, диаграмма направленности сложной антенны определяется произведением двух множителей: диаграммы одного элемента на множитель решетки
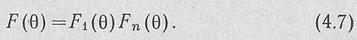
Диаграмма одного элемнта практически всегда широкая, поэтому диаграмма направленности систёмы в основном определяется множителем решетки. В дальнейшем рассматривается методика расчета только одного множителя решетки  , хотя при окончательном расчете диаграммы направленности ее надо рассчитывать по формуле (4.7).
, хотя при окончательном расчете диаграммы направленности ее надо рассчитывать по формуле (4.7).
Если луч направлен по нормали ( 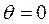 ), то расстояние между излучателями d должно выбираться из условия
), то расстояние между излучателями d должно выбираться из условия

Выполнение неравенства 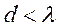 необходимо для того, чтобы диаграмма направленности имела один максимум.
необходимо для того, чтобы диаграмма направленности имела один максимум.
Левое неравенство присуще именно оптимальной антенне.
При d< 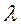 /2 распределение тока в антенне существенно усложняется. Токи в излучателях становятся большими по амплитуде и знакопеременными по фазе и при значительной- уменьшении расстояния d по сравнению с
/2 распределение тока в антенне существенно усложняется. Токи в излучателях становятся большими по амплитуде и знакопеременными по фазе и при значительной- уменьшении расстояния d по сравнению с  можно, получить сверхнаправленную антенну.
можно, получить сверхнаправленную антенну.
Придадим полиному Чебышева вид диаграммы направленности, для чего заменим переменные
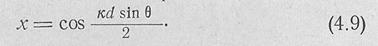
Здесь 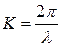 —коэффициент фазы, остальные обозначения
—коэффициент фазы, остальные обозначения
ясны из рис. 4,3. Тогда множитель решетки будет описываться формулами:
при четном числе излучателей 2N
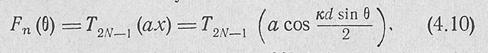
при нечетном числе излучателей 2N + 1
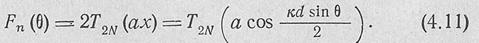
Наивысшая степень полинома m всегда на еденицу меньше числа излучателей.Нормируем диаграмму направленности.Тогда уровень боковых лепестков будет

Часто уровень боковых лепестков выражают в децибелах:
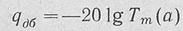
Положение максимумов боковых лепестков определяется по формуле
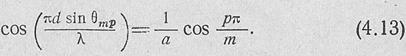
Положение нулей диаграммы можно найти из выражения
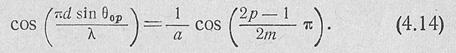
Здесь р — порядковый номер нуля или максимума.
Половина ширины главного лепестка на нулевом уровне получится из (4.14), если положить р = 1:
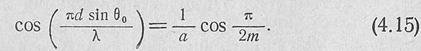
Ширииу диаграммы направленности на уровне половинной мощности можно определить по одной из формул
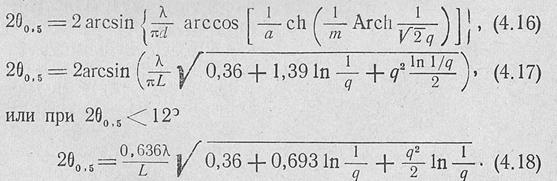
Здесь L — длина антенны.
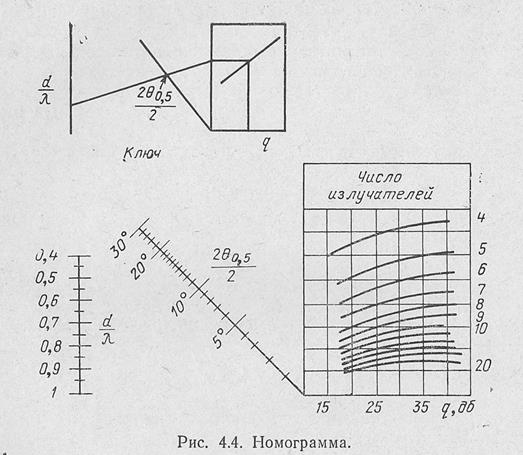
Для облегчения расчетов- по формуле (4.16) 'На рис. 4.4 приведена номограмма- связывающая между собой половину ширины луча на уровне половинной мощности, расстояние между излучателями и уровень боко-
|
|
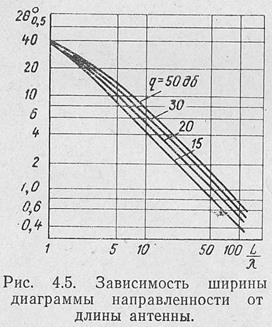
вых лепестков [Л2]. Порядок (пользования номограммой поясняется ключом, приведенным на том же рисунке.На рис. 4.5 приведены зависимости ширины диаграммы направленности на уровне половинной мощности от длины антенны при различном уровне боковых лепест ков, рассчитанные по формуле (4.17). На этом рисунке хорошо видно,
что с уменьшением уров-
ня боковых лепестков
расширяется главный ма-
ксимум; и чем длиннее ан-
тенна, тем больше это
расширение.Важным параметром
антенны с Оптимальной
даграммой является па-
раметр а. Из формул
(4.12), (4.14) следует, что
при известном числе излу-
чателей (степени поли-
нома т) а определяет уровень боковых лепестков и ширину луча.
Если задан уровень боковых лепестков q, то параметр а определяется по одной из следующих формул:
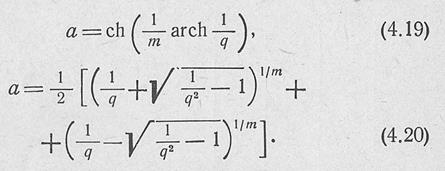
|
При большом числе излучателей и большой величине 1/q справедливо приближенное равенство
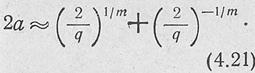
|
|
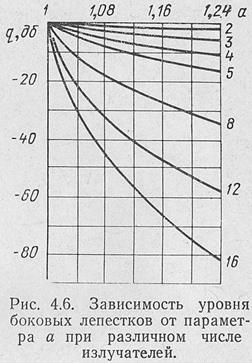
На рис.4.6 представлены зависимости уровня боковых лепестков от параметра а при различном числе излучателей, рассчитанные по формуле (4.19) {Л5]. Из рисунка следует, что чем больше а, тем меньше уровень боковых лепестков.
| Если .задана ширина диаграммы направленности на нулевом уровне, параметр а определяется формулой |
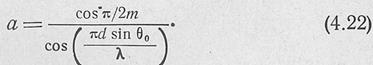
Токи в излучателях вычисляются по формулам: при четном числе излучателей 2N
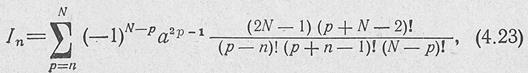
|
при нечетном числе излучателей 2N+1
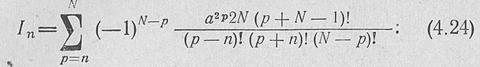
Формулы (4.23),. (4.24) удобны для расчета най ЭВМ.
|
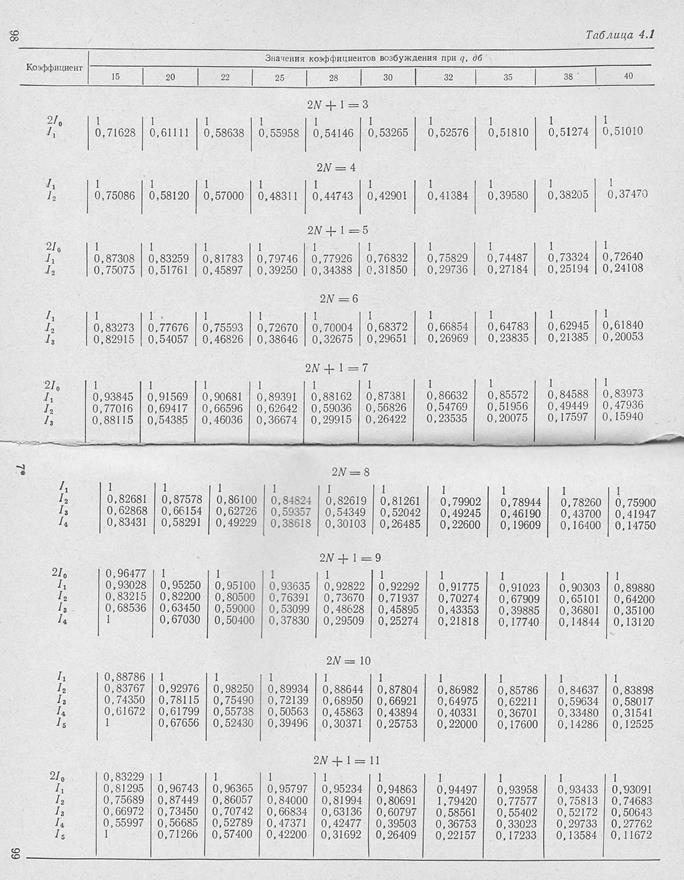
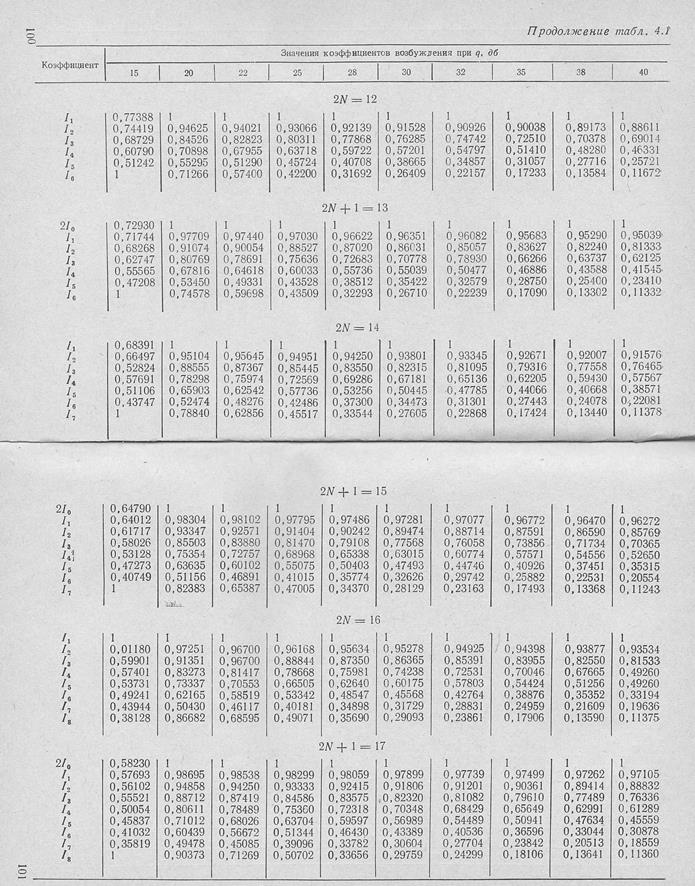
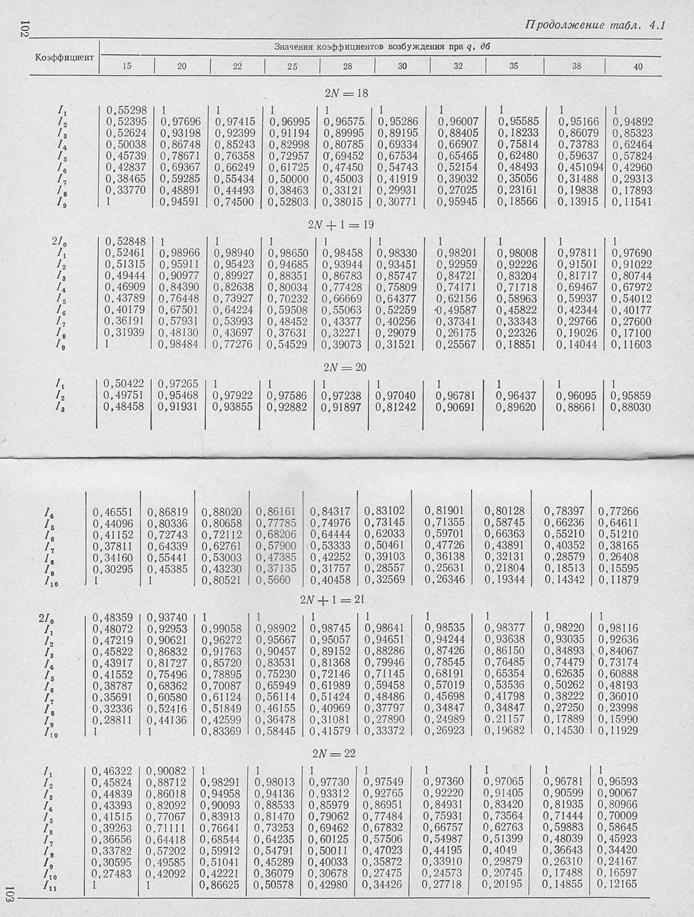
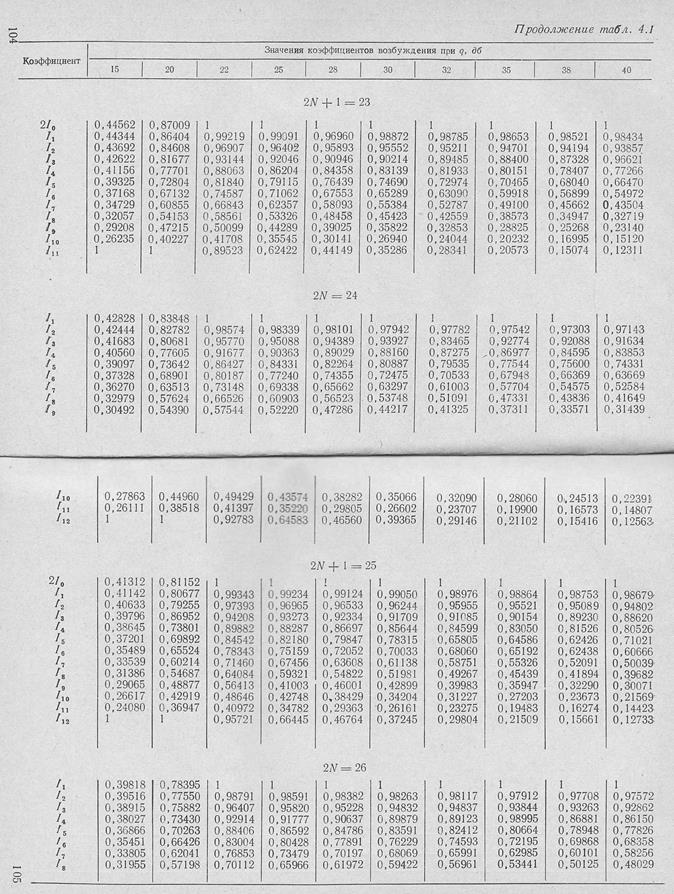
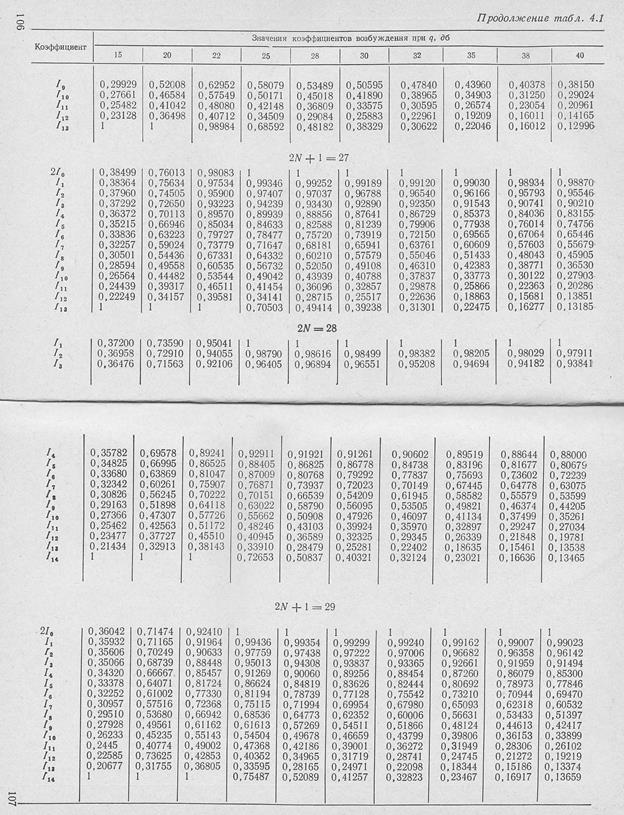
Однако при большом числе излучателей расчет токов по. этим формулам становится весьма громоздким,. Для облегчения расчетёв в табл. 4.1 приведены вычисленные по (Этим формулам относительные величины токов в излучателях- при разном уровне боковых лепестков и различном числе излучателей |Л2].
Если число излучателей превышает 20, то токи в них можно вычислить по приближенной формуле, которая обеспечивает точность в несколько процентов;
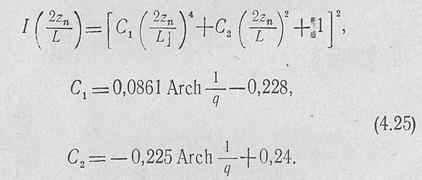 Здесь L — общая длина антенны; zn — расстояние от начала координат до n-го излучателя.Формула (4.25) позволяет просто определить токи во всех излучателях, кроме крайних.Токи в крайних излучателях определяются через токи в предпоследних излучателях:
Здесь L — общая длина антенны; zn — расстояние от начала координат до n-го излучателя.Формула (4.25) позволяет просто определить токи во всех излучателях, кроме крайних.Токи в крайних излучателях определяются через токи в предпоследних излучателях:
при четном числе излучателей 2N
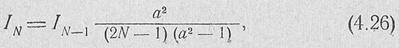
 |
при нечётном числе излучателей 2N +1
|
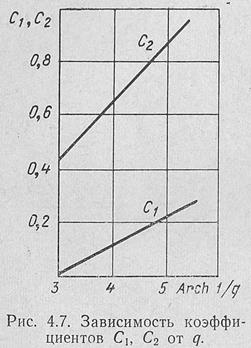
Для облегчения расчетов на рис. 4.7 приведена зависимость коэффициентов C1 и С2 от уровня боковых лепестков q.
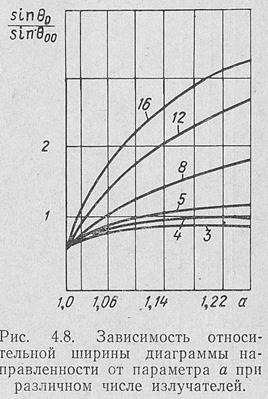
Амплитудное распределение тока вдоль антенный с оптимальной диаграммой существенно «не- равномерное. Соответственно ширина луча. всегда больше, чем у обычной синфазной антенны с одинаковыми токами в излучателях. Для примера на рис. 4.8 приведено отношение синусов половины ширины луча на нулевом уровне оптимальной антенны и антенны с равномерным амплитудным распределением в зависимости от параметра а, т. е. от уровня боковых лепестков.
Из рис. 4.8 следует, что, чем меньше уровень боковых лепестков (больше а), тем больше разница в ширине диаграмм.
К. н. д. -оптимальных антенн :так же . всегда меньше, чем у антенн с одинаковыми токами в излучателях. Боковые лепестки. хотя имеют и малую величину, но их много и все -они одинаковой амплитуды. Соответственно доля мощности, рассеиваемая боковыми лепестками, оказывается большой.
|
|
|
|
|

К. н. д. антенны с оптимальной диаграммой вычисляется по известным токам в излучателях. Однако этот расчет весьма громоздок и здесь не приводится. Расчет К. н. д. можно найти в [ЛЗ]. Ориентировочно величину к. н. д: линейной решетки, состоящей из ненаправленных излучателей, можно оценить по формуле
 |
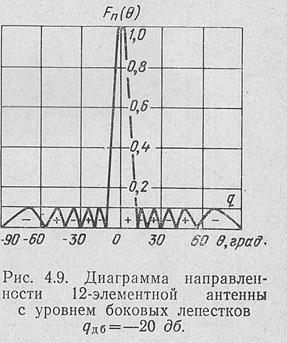
Для примера на рис. 4.9 приведена диаграмма направленности оптимальной антенны, состоящей из 12 изотропных излучателей, размещенных на расстоянии К/2 друг от друга. Уровень боковьгх лепестков тавляет qd6 = —20 дб, что соответствует а=1,037. Уравнение,описывающее эту диаграмму, имеет вид
Диаграмма направленности, изображенная на рис. 4.9, представляет собой, по сути дела, график полинома Тн (ах), представленный на рис. 4.2, только аргументом функции Т11 здесь является не переменная х, а угол 0.
Дата добавления: 2015-06-27; просмотров: 3108;
