Определение формульной единицы
Формульная единица (Z) – это количество атомов, ионов, молекул, принадлежащих одной элементарной ячейке.
При подсчете формульной единицы следует учитывать следующее:
- атом, находящийся в вершине элементарной ячейки, принадлежит одновременно 8 ячейкам, поэтому одной ячейке он принадлежит на 1/8 часть;
- атом, лежащий на гране ячейки, принадлежит ячейке на ½ часть;
- атом, находящийся внутри ячейки, принадлежит ей нацело (то есть на единицу);
- атом, находящийся на ребре – на ¼ часть.
Количество атомов, принадлежащих 1-й элементарной ячейке для различных типов решеток Браве, рассчитывается следующим образом:
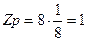
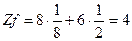

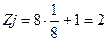
Связь между плотностью вещества d, количеством атомов, принадлежащих одной элементарной ячейке Z, и объемом ячейки V, выражается следующей формулой:
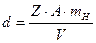
A – атомная масса вещества
mH - масса атома водорода, 1,65×10-24 г
7.3 Координационные числа и координационные многогранники
Координационным числом называют число атомов или ионов противоположного знака, находящихся в ближайшем окружении атома или иона, принятого за центральный. Ближайшее окружение – атомы или ионы, находящиеся на минимально равных расстояниях от центрального атома. Геометрическая фигура, образующая при соединении центров атомов ближайшего окружения называется координационным многогранником.
Координационные числа в структурах кристаллов в значительной степени определяются природой сил, действующих между частицами, т.е. типом связи . Структуры металлоидов обладают наименьшими координационными числами 3-4 (ковалентная связь). Металлические структуры стремятся к высокой координации 12 и8 (металлическая связь). К высокой координации стремятся также и ионные кристаллы, в которых каждый ион старается окружить себя максимальным числом противоположно-заряженных частиц 6-8 (ионная связь)
Согласно правилу Гольдшмидта, устойчивость ионных структур определяется соотношением радиусов катионов к радиусу анионов. Устойчивой считается та структура, которая исключает соприкосновение одноименно заряженных сфер (рис. 7.2).
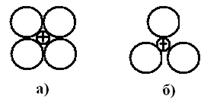
Рисунок 7.2 – Пример неустойчивой (а) и устойчивой (б) ионной структуры
Таблица 7.2 – Зависимость координационного числа и координационного многогранника от соотношения радиуса rк/ rа
| Координационное число | Координационный многогранник | Пределы отношений rк/ rа |
| Гантель | 0 ÷ 0,15 | |
| Треугольник | 0,15 ÷ 0,22 | |
| Тетраэдр | 0,22 ÷ 0,41 | |
| Октаэдр | 0,41 ÷ 0,73 | |
| Куб | 0,73 ÷ 1,0 | |
| Кубоктаэдр | более 1,0 |
Капустинский А.Ф. 30-годах прошлого столетия высказал предположение, что в природе наиболее распространены соединения с четными к.ч.: 4,6,8,12. Нечетные к.ч. 3,5,7,9,11 – менее распространены и играют незначительную роль.
Координационные многогранника могут быть и более сложными по форме (например, трехшапочная тригональная призма, ромбододекаэдр, притупленный октаэдр и др.). Одному и тому же координационному числу могут соответствовать различные виды координационных многогранников. Например: к.ч. 6 – октаэдр и тетрагональная призма.
В простых бинарных соединениях по соотношениям координационных чисел можно определить химическую формулу, пользуясь правилом: обратные отношения координационных чисел соответствуют количеству элементов в химической формуле.
 К.ч. Si/O = 4 2
К.ч. Si/O = 4 2
К.ч. O/Si = 2 1
SiO2 – кварц
Таким образом, можно проверить правильность найденных координационных чисел или определить химическую формулу вещества.
ГЛАВА 8. Плотнейшие упаковки
Дата добавления: 2015-06-27; просмотров: 2386;
