Основные операции над тензорами

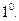Сложение и вычитание тензоров. Определяется для тензоров одинакового типа, как покоординатное сложение и вычитание.

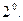Умножение тензора на число. Определяется для любых тензоров. Умножается каждая координата тензора на число.

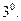Умножение тензоров. Определяется для любых тензоров,заданными своими координатами в некотором (общем) базисе.

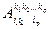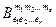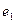
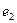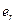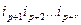Чтобы умножить тензор А с координатами на тензор В с координатами надо в тензоре В переименовать индексы … на , а индексы на 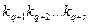и составить тензор D типа (p+r,q+s) с координатами = .

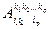
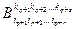Замечание:операция умножения тензоров, вообще говоря, не коммутативна: АВ 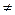ВА. (хотя элементы и одинаковые, но порядок их, вообще говоря, разный).

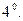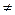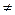Свёртка тензора: Применяется для тензоров типа (p,q) где p 0, q 0.

Среди индексов тензора отмечается один верхний индекс и один нижний, заменяются одной буквой и производят суммирование по этому индексу согласно соглашению. Свертка тензора переводит тензор типа (p,q) в тензор типа (p-1,q-1) т.е. понижает его ранг на 2.

Замечание:Термин свертка можно применить и к паре перемножаемых тензоров А и В, когда у одного тензора отмечается верхний индекс, а другого нижний и по этим индексам производится суммирование.

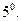Симметрирование тензора по паре нижних индексов (или верхних).

( + )

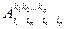
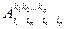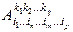Аналогично для пары верхних индексов.

Получаемый тензор симметричен по указанной паре индексов.

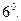Альтернирование тензора по паре нижних индексов (или верхних).

( - )

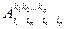
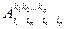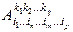Аналогично для пары верхних индексов.

Получаем тензор кососимметричный по указанной паре индексов.