Е3(–1/2, 1/2, 1/2) е3¢(0, 0, 1) .

Построение: ;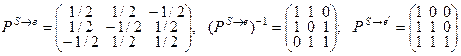

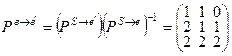и кроме того: 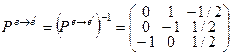. Если обозначить P^е®e¢=Р₃, P^е¢®e =Р₄, то Р₃e¹ = e^1¢; Р₃e² = e^2¢; Р₃e³ = e^3¢; Р₄e^1¢ = e¹; Р₄e^2¢ = e²; Р₄e^3¢ = e³. Для Р₁, Р₂, Р₃, Р₄ справедливы те же соотношения, что и для В₁, В₂, В₃, В₄:

В₁; В₂ = 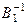; В₃ = 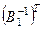; В₄ = ;

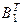Р₁; Р₂ = 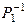; Р₃ = 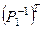; Р₄ = .

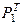Вопрос: Почему же В₁ и Р₁ (а также остальные) матрицы различны? Правда, они симметричны относительно второй большой диагонали?

Попробуйте ответить на этот вопрос прежде чем вы прочитаете последующие две строчки.

Ответ: Матрицы 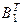и матрицы Р₁ это одна и та же матрица перехода но Р₁ в стандартном базисе, а 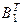в базисе {e_i}.

Пусть xÎE_n.Пусть в базисе {e_i¢, e^i¢} x = x_i¢eⁱ т.е. x_i¢ ковариантные координаты вектора x.

x_i¢ = (x,e_i¢) = 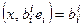(x,e_i) = 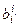x_i, т.е. x_i¢ = 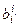x_i.

При переходе к новому базису ковариантные координаты вектора x преобразуются с помощью матрицы перехода 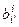от базиса {e_i} к базису {e^i¢} (т.е. так же как координаты базисных векторов). Этим и обусловлено название – ковариантные (согласованные) .

Кроме того : x^i¢ = (x,e^i¢) = 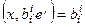(x,e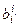ⁱ) = xⁱ.

При переходе к новому базису контравариантные координаты вектора x преобразуются с помощью матрицы перехода 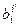от базиса нового к старому. Это несогласование преобразований и обусловило название контравариантные (несогласованные) координаты.

Задача. Вектор х(5, 2, 1) в базисе {e₁(1, 1, 0), e₂(0, 1, 1), e₃(0, 1, 1), e¹(1/2, 1/2, 1/2), e²(1/2, –1/2, 1/2), e³(–1/2, 1/2, 1/2)} имеет ковариантные координаты (7, 6, 3) и контравариантные координаты (3, 2, –1). Это было установлено при решении задач в предыдущем параграфе . Найти ковариантные и контравариантные координаты этого же вектора в базисе {e_1¢(1, 0, 0), e_2¢(–1, 1, 0), e_3¢(0, –1, 1), e^1¢(1, 1, 1), e^2¢(0, 1, 1), e^3¢(0, 0, 1)}.

◀ Как известно, ковариантные и контравариантные координаты вектора х преобразуются по-разному: с помощью формул: x_i¢ = 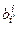x_i и x^i¢ = 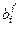x_i, тогда x_i¢ = 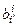x_i Þ 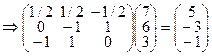, т.е. х¢ = 5е^1¢ – 3е^2¢ – е³¢ (это х(5, 2, 1)). Итак (7, 6, 3) ® (5, –3, –1) для ковариантных координат.

Далее: 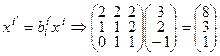, т.е. х¢ = 8е_1¢ + 3е_2¢ + е_3¢ (это х(5, 2, 1)). Итак (3, 2, –1) ® (8, 3, 1) для контравариантных координат.

Здесь матрицы перехода взяты из предыдущей задачи. ▶